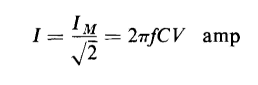| Capacitors, Magnetic Circuits, and Transformers is a free introductory textbook on the physics of capacitors, coils, and transformers. See the editorial for more information.... |

|

Home  Capacitance and Related Effects Capacitance and Related Effects  kVA Rating of Capacitors kVA Rating of Capacitors |
|||||||||||






|
|||||||||||
kVA Rating of Capacitors
Capacitors are used in electric transmission and distribution systems for power factor correction. Present loads on electric power systems are predominantly inductive and therefore take current that lags the voltage. Losses in transformers, transmission lines, and generators are lower for a given amount of real power when the power factor is near unity than when the current lags the voltage by an appreciable angle. The over-all power factor of a system that normally delivers current to an inductive load can be improved by installing capacitors at various locations in such a system. The amount of capacitance to be installed for a given improvement in the power factor is a function of the amount of reactive power taken by the system. Reactive power is measured in vars or kilovars and capacitors used for power factor correction are rated in kilovars. Consider an ideal capacitor, i.e., one in which there are no energy losses. Let C = the capacitance of the capacitor in farads Under steady-state a-c operation the instantaneous voltage applied to the capacitor is expressed by
and the instantaneous current in the capacitor is
then substitution of Eq. 2-65 in 2-66 yields
where ω = 2πf. The maximum value of the instantaneous current expressed by Eq. 2-67 occurs when cos ωt is unity, and we have
The rms or effective value of a sinusoidal current is maximum value divided by
The kilovar rating of the capacitor is the product of the rated current at rated frequency and the rated voltage divided by 1000, hence
|
|||||||||||
Home  Capacitance and Related Effects Capacitance and Related Effects  kVA Rating of Capacitors kVA Rating of Capacitors |
|||||||||||
Last Update: 2011-01-10


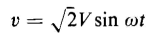


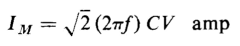
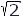 , and from Eq. 2-68 we get the rated current
, and from Eq. 2-68 we get the rated current