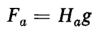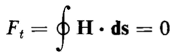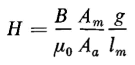Demagnetization Curve

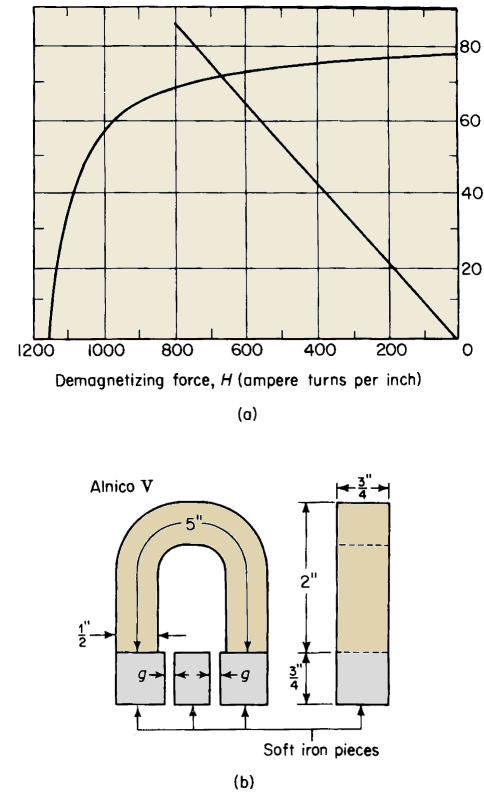
Permanent magnets operate in that region of the hysteresis loop known as the demagnetization curve. The greater the area under the demagnetization curve the more effective is the material in the permanent magnet. Figure 3-29 shows a U-shaped magnet with a soft iron bar, sometimes called a keeper, across its open ends. The magnet is provided with an exciting winding that is usually removed after the magnet has been magnetized. It is common practice to use only one turn with a correspondingly heavy current, which is applied for only a fraction of a second.

Let

N = the number turns in the winding
l = the mean length of the permanent magnet (the U-shaped portion only)

Suppose that for the condition depicted in Fig. 3-29(a) a current i is applied to the winding such that the magnetizing force is H_max in Fig. 3-30, which shows the curve for the magnetic material. Then H_max = NI/l if the reluctance of the horizontal soft iron piece is neglected.

Figure 3-29. Magnetized U-shaped magnet (a) without air gap and with current in magnetizing direction, (b) without air gap and with current in demagnetizing direction, (c) with air gap and without current

The corresponding flux density throughout the permanent magnet is B_max if leakage is neglected. If the current is reduced to zero, the magnetizing force becomes zero and the flux density drops from the value B_max to B_r, the retentivity. In order to reduce the flux density to zero it is necessary to apply a current in the reverse direction as shown in Fig. 3-29(b) of such a value as to produce a magnetizing force equal to the coercivity H_c in Fig. 3-30. The portion B_RPH_C of the curve is known as the demagnetization curve; it represents the region of interest in the operation of permanent magnets.

Figure 3-30. Curve of a permanent magnet material

Suppose that the magnetizing force H_max has been applied to the magnet with the current in the direction shown in Fig. 3-29(a). Then if the current is reduced to zero, without in the meantime reversing its direction, the flux density will not drop to zero but rather to the value B_r as mentioned previously and its direction will remain unchanged. If now a current of such a

value as to produce a magnetizing force H in Fig. 3-30 is passed through the winding in the reverse direction as shown in Fig. 3-29(b), the flux density drops from its value of B_r to B. It is important to note that although the direction of the current in Fig. 3-29(b) is opposite that in Fig. 3-29(a) the direction of the flux density is the same in both cases.

The same magnetic state, i.e., a reduction in the flux density from the value B_r to that of B can be produced when there is no current in the winding by introducing an air gap g of the proper length into the magnetic circuit as shown in Fig. 3-29(c), assuming that leakage can be neglected. This can be shown as follows

Let

l_m = the mean length of the permanent magnet
A_m = the cross-sectional area of the magnet
H = the magnetizing force for the permanent magnet material (see Fig. 3-30)
B = the magnetic flux density in the permanent magnet material (see Fig. 3-30)
g = the length of the air gap
A_a = the cross-sectional area of the air gap, which does not need to be the same as the cross-sectional area Am of the magnet
H_a = the magnetizing force for the air gap

The reluctance of the soft iron pieces on both sides of the air gap is neglected. The mmf for the air gap is

[3-75]

and the mmf for the permanent magnet is

[3-76]

The total mmf F_t around the closed flux path must be the sum of these two mmfs, i.e.

[3-77]

Since for the condition represented by Fig. 3-29(c) there is no current in the exciting winding, the total mmfFt must be zero in accordance with Eq. 3-34. Hence

[3-78]

Then from Eqs. 3-77 and 3-78 there results

[3-79]

Figure 3-31. (a) Demagnetization curve for Alnico V; (b) alnico magnet with soft iron pieces and air gaps

The magnetizing force H for the magnet is obtained in terms of H_a, the magnetizing force for the air gap, by comparing Eqs. 3-75 and 3-76 with Eq. 3-79 and is found to be

[3-80]

which can be expressed by

[3-81]

This relationship is represented graphically by the straight line OP in Fig. 3-30. The values of the magnetizing force H and the flux density B for the permanent magnet are determined by the intersection of the line OP with the demagnetization curve. On the basis of no magnetic leakage the flux must be the same in all parts of the magnetic circuit, i.e., in the permanent magnet, in the soft iron pieces, and in the air gap. The flux is expressed by

[3-82]

Example 3-5:

Figure 3-31 (a) shows the demagnetization curve for the Alnico magnet of Figure 3-3 l(b). The length of each of the two air gaps in Fig. 3-3 l(b) is g = 0.10 in. Neglect leakage but allow for fringing at the air gaps and determine the flux in the air gaps.

Solution:

The flux density in the permanent magnet is determined by making use of the graphical construction illustrated in Fig. 3-30. The values to be used in Eq. 3-81 are This is the equation of a straight line, which when plotted in Fig. 3-31 (a) intersects the demagnetization curve at approximately B = 72 kilolines per sq in. and H = 660 amp turns per in. Hence Φ = BAm = 72,000 x 0.375 = 27,000 maxwells