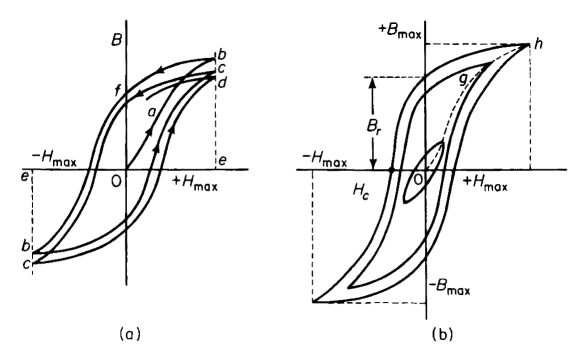
Hysteresis Loop

The nonlinear relationship between the magnetic field intensity, also known as the magnetizing force, and the magnetic flux density in ferromagnetic materials is of great importance in engineering applications. In some cases this nonlinearity is undesirable since it may produce distortion of currents and voltages in a-c circuits. There is also the hysteresis loss, which is proportional to the area of the loop, (see Fig. 3-13) and the number of cycles that the flux undergoes in a given period of time. However, there are other applications in which this nonlinear characteristic is highly desirable if not altogether indispensable. Permanent magnets would not exist if the flux density B would return to zero when the magnetizing force H is removed. Self-excited d-c generators require operation of their magnetic circuits in the saturated region. Magnetic amplifiers, peaking transformers, and other devices depend for their operation upon nonlinear characteristics of magnetic materials.

Consider the case of the toroid in Fig. 3-9(a) as a completely unmagnetized ferromagnetic material. Let a current be passed through the winding in the direction shown. A magnetic flux will then be set up in the core, let us say in the positive direction. As this current is increased further the flux increases, rapidly at first, but beyond a certain value of current or H, the increase is less and less for a given increase in H. The curve oab of Fig. 3-26(a) indicates the approximate relation between the flux density and the magnetizing force. Suppose that the current is increased to a certain maximum value for which the corresponding value of the magnetizing force is +H_max, then the flux density reaches a maximum value eb in Fig. 3-26(a). If the current is now decreased to zero, the flux density does not drop to zero but to a value of 0f shown in Fig. 3-26(a). Reversing the current and with the same max value it had before produces the magnetizing force -H_max, and the flux density e'b'. If the current is reversed and the same maximum value is applied the flux density will not return to its former positive maximum value of eb but to a somewhat lower value ec. Similarly the succeeding negative value will be e'c'. After applying alternate equal values of +H_max and -H_max a number of times, a process known as cycling, the magnitude of the flux density +B_max will equal that of -B_max and the loop known as the hysteresis loop will be symmetrical. A family of three hysteresis loops is shown in Fig. 3-26(b). If the ferromagnetic material is worked through a number of smaller loops the positive tips of the loops will lie on the curve ogh in Fig. 3-26(b). The curve ogh is called the normal magnetization curve.

Figure 3-26. (a) B-H characteristic of initially unmagnetized iron; (b) hysteresis loops.

The flux density B_r, which is still present after the magnetizing force is reduced to zero, is called the residual flux density. The magnetizing force H_c required to reduce the flux density from the residual value B_r to zero is called the coercive force. These two quantities, i.e., residual flux density and coercive force are of great importance in permanent magnets.