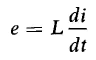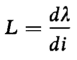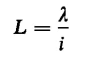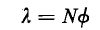Self-Inductance

The voltage impressed on a series inductive circuit in which the capacitance effects are negligible and in which there are no thermal or electrolytic sources of emf, is expressed by

where

v = the applied voltage in volts
i = the current in amperes
R = the resistance in ohms
A = the magnetic flux linkage in weber turns
t = time in seconds

The flux linkage λ may be due only to the current i in the circuit itself; in addition it may be due to currents in other circuits that are coupled magnetically with the circuit under discussion. For that matter a permanent magnet in the vicinity of the circuit may contribute flux linkage also.

If, however, the flux linkage λ is produced solely by the current i in the circuit itself and if the relationship between λ. and i is a linear function, then the expression for the applied voltage becomes

[4-1]

where L = self-inductance in henries. Figure 4-1 shows a schematic diagram of an inductive circuit. The dotted lines indicate the magnetic flux.

Figure 4-1. Circuit with resistance and self-inductance

The voltage that is induced by the time variations in the current of a circuit is called the electromotive force of self-induction, or simply the emf of self-induction, and is expressed in terms of the self-inductance by

[4-2]

The flux linkage λ can be a linear function of the current i only if the self-inductance L is constant. In circuits where the self-inductance is a variable, as for example in the case of electromagnets with variable length of air gaps as well as in some generators, the time variation of the self-inductance will affect the voltage and must be taken into account. Circuits with variable inductance will be discussed later in this chapter.

The emf induced in a circuit can always be expressed by

[4-3]

This is true whether L is a constant or a variable, or whether the flux linkage λ is produced solely by the current in that circuit or whether currents in other circuits contribute to the flux linkage as well.

However, if the self-inductance is constant and the only flux linkage is the one resulting from the current i in the circuit itself, then Eq. 4-2 can be equated to Eq. 4-3 with the result that

[4-4]

from which

[4-5]

and

[4-6]

Equation 4-6 defines inductance as the flux linkage per ampere. Consider the toroid shown in Fig. 3-9 and assume the thickness R₂ - R₁ to be small compared with R₁. Then the expression for the flux produced by the current i in the winding is

[4-7]

which can be reduced to the more general form

[4-8]

where A is the cross-sectional area of the flux path and l is the length of the flux path. When all of the flux Φ links all the turns N the flux linkage is

The flux Φ in the toroid links all N turns, so that on the basis of Eqs. 4-6 and 4-8 the self-inductance is

[4-9]

The permeability for an air core is μ = μ₀ = 4π x 10^-7 h per m, and the expression for self-inductance if the core has a uniform cross-sectional area becomes

[4-10]

If the core material has constant relative permeability of μ_r then the self-inductance is given by

[4-11]

When both sides of Eq. 4-9 are multiplied by i²/2 the result expresses the energy stored in the field thus

[4-12]

where

[4-13]

Substitution of Eq. 4-13 in Eq. 4-12 yields

[4-14]

The term Vol HB/2 is the value of the energy stored magnetically in volume Vol. When Eq. 4-6 is substituted in Eq. 4-14 the energy that is stored magnetically can be expressed in terms of flux linkage and current as follows

[4-15]

Equations 4-14 and 4-15 apply only to the case of core materials that have constant permeability. There is the further restriction on Eq. 4-14 that the flux density B is practically uniform throughout the core.