| Capacitors, Magnetic Circuits, and Transformers is a free introductory textbook on the physics of capacitors, coils, and transformers. See the editorial for more information.... |

|

Home  Magnetic Circuits Magnetic Circuits  Magnetic Flux and Magnetic Lines of Force Magnetic Flux and Magnetic Lines of Force |
|||||||||||||






|
|||||||||||||
Magnetic Flux and Magnetic Lines of Force
In Chapter 2 the concept of electric flux was used in connection with the electric field in which the electric flux density at a point in free space is directly proportional to the electric field intensity at that point. Analogous relations exist for the magnetic field in that the magnetic flux density at a point in free space is directly proportional to the magnetic field intensity at that point, as expressed by
where B = magnetic flux density and μ0 = magnetic permeability of free space. In the rationalized MKS μ0 has the value of 4π x 10-7 henry per meter and B is expressed in webers per square meter. The magnetic field is a field of force and requires energy for its production. A magnet when brought into the magnetic field produced by another magnet or by a current in a circuit experiences a force. Although a positive or negative charge can be isolated, a magnetic pole cannot exist by itself since every magnet has an equal number of poles of opposite polarity. The simplest magnet has one north pole and one south pole. However, if a north pole could exist by itself without the accompanying south pole, and this north pole were brought to within a distance of r1 of the filament in Fig. 3-2, it would experience a force in a direction tangent to the circle of radius r1 as determined by the right-hand rule. The locus of constant force would be a cylinder of radius r1 concentric with the filament. The magnetic field can therefore be represented by lines of force.
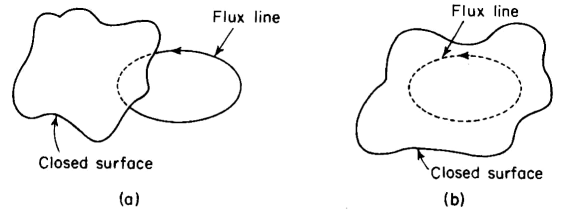
It will be recalled that the flux lines in an electric field emanate from a positively charged body and terminate on a negatively charged body. The magnetic flux lines produced by the current in the straight conductor close upon themselves forming circles concentric with the conductor. In less simple arrangements of current-carrying conductors the magnetic flux lines close upon themselves although they do not necessarily form circles. Because of the property of the magnetic flux lines closing upon themselves (a) the number of magnetic flux lines that enter a closed surface in the field must also leave that surface or (b) the flux lines within a closed surface are completely enclosed by that surface as shown in Fig. 3-4(a) and (b). This law is expressed mathematically by
The surface integral in Eq. 3-16 merely states that the net magnetic flux emanating from a closed surface is zero. Figure 3-5 shows an infinitesimal surface of area dA in a magnetic field. The flux density in this surface is B and the direction of the flux is at an angle Θ with the normal. The magnetic flux passing through this infinitesimal area is given in vector notation by
The flux through a finite surface would be
The difference between the integral of Eq. 3-16 and that of Eq. 3-17 is that the former is taken over a completely closed surface whereas that of
Eq. 3-17 is taken over a surface that does not close upon itself if Φ is to have a value other than zero.
|
|||||||||||||
Home  Magnetic Circuits Magnetic Circuits  Magnetic Flux and Magnetic Lines of Force Magnetic Flux and Magnetic Lines of Force |
|||||||||||||
Last Update: 2011-02-16