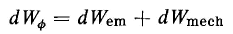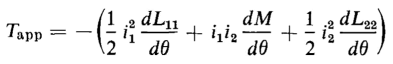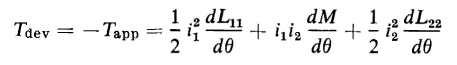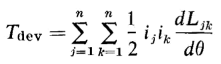Torque and Force in Inductively Coupled Circuits

It is evident from Eqs. 4-58 and 4-59 that the energy stored in the magnetic field associated with two or more magnetically coupled circuits can be varied by changing the current in one or more of the circuits, or by changing one or more of the self-inductances or mutual inductances. If all currents are held constant, mechanical work is involved in changing the stored energy; this necessitates a change in one or more of the inductances. The rotary electromagnet in Fig. 4-5 illustrates two inductively or magnetically coupled circuits and in which the reluctance of the iron is considered negligible in comparison with that of the air gaps between the stator and the rotor. When the currents i₁ and i₂ are flowing in circuits 1 and 2 in the directions shown, and with the angle θ smaller than 90°, the magnetic forces develop torque in the counterclockwise direction. Mechanical energy input is required to increase θ. This means that torque must be applied counterclockwise. If the angle θ is increased by the differential amount dθ, and the applied torque is dθ, then the mechanical differential energy input is

Figure 4-5. Coupled circuits with variable self- and mutual inductance

[4-60]

If, at the same time, there is an electromagnetic differential energy input dW_em, the energy stored in the field will be increased by the differential amount

[4-61]

When the differentiation in Eq. 4-56 is performed, the expression for the electromechanical differential energy becomes

[4-62]

It should be noted that the inductances L₁₁, L₂₂, and M are not constant but are functions of the angle θ.

The energy stored in the field is given by Eq. 4-58 and it will be remembered that the energy stored in the field can be changed by a change in one or both of the currents as well as by a change in one or all of the inductances, so that the differential energy input to the magnetic field can be written as

[4-63]

When Eq. 4-63 is subtracted from 4-62, then, on the basis of Eq. 4-61, the mechanical differential energy input to the energy stored in the field is found to be

[4-64]

and, according to Eq. 4-60, the applied torque must be

[4-65]

The magnet develops a torque equal and opposite to the applied torque, that is

Similarly the developed force for a linear displacement is given by

[4-66]

When there are n-coupled circuits instead of 2-coupled circuits, and there is only one movable member in the electromagnet, as in the case of conventional motors and generators, the torque is found on the basis of Eq. 4-59 to be

[4-67]

If the change in inductance takes place while the currents are held constant, one-half of the electromagnetic energy input is stored in the magnetic field, whereas the other half is converted into mechanical energy. This is evident from Eqs. 4-63 and 4-64 because for constant currents, di₁ and di₂ must be zero. This equal division of stored energy and mechanical energy with constant currents is true only for linear circuits and does not hold for nonlinear magnetic circuits, i.e., where there is appreciable saturation.

On the other hand, if the flux linkages are held constant while there is a change of inductance, the electromagnetic energy input must equal zero as is shown by Eq. 4-54 for dλ₁ and dλ₂ = 0. In that case energy stored in the field is given up to be converted into mechanical energy, i.e., the mechanical energy is abstracted from the energy absorbed in the field.