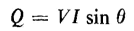Reactive Power

The real power in a-c circuits under steady conditions is the average of the instantaneous power taken over an integral number of half cycles and is expressed by

[4-101]

where Θ is the angle by which the current lags or leads the voltage. It is evident from Eq. 4-101 and Figs. 4-8(b) and 4-8(c) that the real power in a purely inductive circuit is zero under steady-state conditions. However, the term reactive power is used to express the product of current and voltage in a circuit in which the real power is zero. In circuits where the current lags the voltage by an angle smaller than 90°, the reactive power consumed by the circuit is

[4-102]

In capacitive circuits the current leads the voltage, and the reactive power consumed by such a circuit is negative. Hence, capacitive circuits generate reactive power and are therefore sources of reactive power. Capacitors are used in industrial power systems to furnish reactive power.

Thus, a circuit comprised of self-inductance, L, in series with a resistance R_eff has an impedance of

[4-103]

and

[4-104]

furthermore

[4-105]

From Eqs. 4-104 and 4-105 it follows that

[4-106]

from which

[4-107]

[4-108]