| Capacitors, Magnetic Circuits, and Transformers is a free introductory textbook on the physics of capacitors, coils, and transformers. See the editorial for more information.... |

|

Home  Inductance - Electromagnetic Energy Conversion Inductance - Electromagnetic Energy Conversion  Inductive Reactance Inductive Reactance |
|||||||






|
|||||||
Inductive Reactance
When an alternating current of constant amplitude is passed through the winding of an air-core inductance, energy is alternately stored and given up every quarter cycle. If the resistance of the circuit is negligible, all of the energy that is stored in the magnetic field during one quarter cycle is reversible and is returned to the source during the following quarter cycle. The average power consumed by such a circuit is zero during a number of complete cycles. Let L = self-inductance in henrys
i =
ω = 2πf If the resistance is negligible, the applied voltage is
In Eq. 4-99, V is the rms value of the voltage applied to the self-inductance. Also
where X is the inductive reactance. From Eqs. 4-98 and 4-99, it is evident that the current lags the voltage by 90°. The relationship between the voltage and current for a circuit of constant self-inductance and negligible resistance is shown in Fig. 4-8(a) and 4-8(c). The instantaneous power is shown graphically as a function of time in Fig. 4-8(b).
|
|||||||
Home  Inductance - Electromagnetic Energy Conversion Inductance - Electromagnetic Energy Conversion  Inductive Reactance Inductive Reactance |
|||||||
Last Update: 2011-01-08


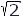 I sin ωt
I sin ωt 

