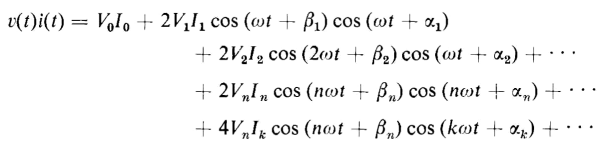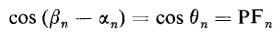Power

The real power consumed in a circuit is the average of the instantaneous values over a given period of time. For a-c circuits, the real power is the average taken over one or more complete cycles. Thus, if a complex voltage wave is expressed by

[5-32]

and a complex current wave by

[5-33]

the real power is then obtained as follows

[5-34]

where the product v(t)i(t) results in the following series

[5-35]

It is not necessary to integrate every term in the series represented in Eq. 5-34 in order to evaluate the series. However, by considering 9 of the several typical terms, the integral can be evaluated in a simpler manner. Let us first consider the first term in the series of Eq. 5-34 as follows

[5-36]

Then consider the product of the n^th voltage harmonic and the n^th current harmonic when n may have any integral value 1, 2, 3, etc.

[5-37]

There is also in Eq. 5-37 the series of cross-products represented by the term

which can be reduced to

[5-38]

The average value of the term above, taken over a complete cycle, is zero. From this it is apparent that the real power associated with a voltage harmonic of a given order and a current harmonic of a different order is zero. Therefore, the expression for the power obtained by carrying out the integration of Eq. 5-33 becomes

[5-39]

In Eq. 5-38, the angle

[5-40]

or the angle by which the n^th current harmonic lags or leads the n^th voltage harmonic, and

[5-41]

where PF_n is the power factor associated with the n^th voltage harmonic and the w^th current harmonic. In the case of a sinusoidal voltage and a non-sinusoidal current, the power is the product of the effective value of the voltage, the effective value of the fundamental in the current, and the cosine of the angle by which the fundamental in the current is displaced from the voltage. The same consideration applies to a sinusoidal current and nonsinus-oidal voltage.