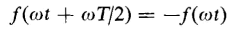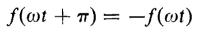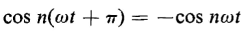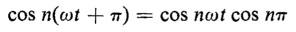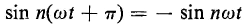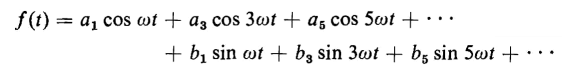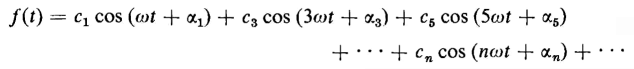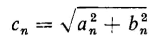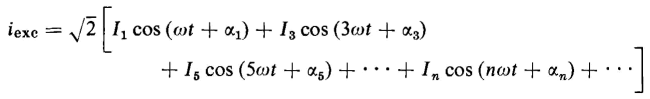Harmonics

Under steady conditions of constant voltage and constant frequency, the current in a reactor, or the exciting current (the no-load current in a transformer), is a periodic function of time. A periodic function can be represented by a Fourier series as follows

[5-20]

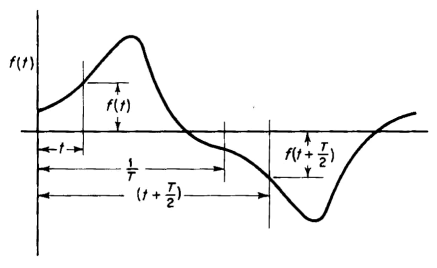
The constant a₀ corresponds to a d-c component. Under steady-state conditions, if the applied voltage does not contain a d-c component, the constant a₀ is equal to zero. With a-c excitation only, the exciting current has symmetrical wave form, i.e., the negative half cycle has the same shape as the positive half cycle. Figure 5-5 shows a symmetrical wave, i.e., one in which f[t + (T/2)] = -f(t).

A symmetrical wave contains odd harmonics only because the presence of even harmonics leads to dissymmetry. Then, for a constant frequency, the angular velocity ω must be constant, and the wave is symmetrical when

[5-21]

In Eq. 5-21, T is the period or the time for the wave to undergo a complete cycle. Hence, ωT = 2π radians, and Eq. 5-21 can be reduced to

[5-22]

Figure 5-5. Symmetrical wave

If the nth harmonic in the cosine series is to satisfy the conditions for symmetry

[5-23]

but

[5-24]

then, from Eqs. 5-23 and 5-24, symmetry requires that

and

[5-25]

Equation 5-24 can be satisfied only if n is odd; as for even values of n, cos nπ is 1. Similarly

[5-26]

only if n is odd.

It follows, therefore, that only odd harmonics are present in a periodic function that is symmetrical, as is the case for an iron-core reactor or the exciting current in an iron-core transformer when the flux wave is symmetrical. Such a current can therefore be represented by omitting a₀ and all the even harmonics in Eq. 5-20 as follows

[5-27]

Equation 5-27 can also be put into the following form

[5-28]

where

[5-29]

[5-30]

Hence, if I₁ is the effective value of the fundamental component of current, and I₃, I₅, etc. are the effective values of the harmonic components, the exciting current can be expressed by

[5-31]

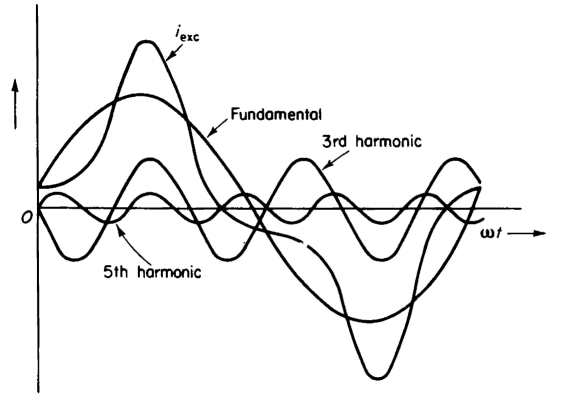
A sinusoidal flux variation with respect to time produces a distorted current in an iron-core reactor or in iron-core transformers, which can be divided into a fundamental component and into odd harmonic components. The third harmonic is the predominating harmonic.

Figure 5-6. Exciting current and its fundamental, 3rd, and 5th harmonic components

The amplitudes of the harmonics generally decrease as the order of the harmonics increases, harmonics of higher orders than the 9^th usually having negligible amplitudes. Figure 5-6 shows a current wave with its fundamental, 3^rd harmonic, and 5^th harmonic components.