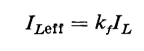Power Output

It should be emphasized that I_L represents the average value of one-half of the load current wave. However, in expressing the power expended in a resistance, the square of the effective value of the current is multiplied by the value of the resistance. The ratio of effective to average value of a periodic current or voltage is called the form factor k_f, which is 1.11 for a sinusoid. The effective value of the load current is therefore

and if the load resistance is R_L ohms, the output is

[7-28]

For a given a-c source voltage V, the output current is a maximum when α = 0, and, if the leakage reactance is neglected, the maximum output current is

[7-29]

where R'_G is the resistance of the gate circuit, which, in the case of the parallel connection, is the resistance of each gate winding, and for the series connection is twice the resistance of each gate winding. The a-c source voltage is assumed to be sinusoidal; therefore, the output current is sinusoidal when α = 0 and k_f = 1.11. The maximum power output is, therefore, approximately

[7-30]

Form factor

When the leakage impedance of the gate windings is neglected, the average value of the output current to a noninductive load resistance is expressed by Eq. 7-25, as follows

[7-31]

The effective rms value of the load current is

[7-32]

and the form factor is the ratio of Eq. 7-32 to Eq. 7-31. This ratio can be reduced to

[7-33]