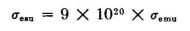Ground Systems for Broadcast Antennas

Author: Edmund A. Laport

Antenna performance is standardized with reference to the ground being a perfectly conducting flat plane. Such an assumption serves a very useful purpose in revealing the ultimate possibilities of a certain radiator in terms of its dimensions and longitudinal and sectional geometry at a given frequency. All practical deviations from this norm are due to a number of empirical circumstances, of which one is the earth itself.

A line of electric force (displacement current) extends from the top of the antenna through surrounding space to the earth. Upon entering a perfectly conducting earth it becomes a conduction current which returns to the base of the antenna and becomes a portion of the antenna current. The electric lines of force of the antenna field are thus seen to be the continuation current of a closed circuit through surrounding space. With a perfectly conducting earth, the electric line of force is always normal to the surface. When the earth is imperfectly conducting, the Hue of force tilts forward in the direction of propagation. This means that the Poynting vector at the surface of the earth is tilted downward and has a component that points into the earth where it is dissipated. The component parallel to the earth represents the power propagated onward in the half space above the ground.

A vertical radiator above natural earth without any sort of ground system, energized by an electromotive force between the antenna and the earth, would require all earth currents to return to the antenna through a very imperfect conductor. The earth is actually an imperfect dielectric in that it has both finite conductivity and inductivity. The range of values encountered in engineering practice in various soils and various amounts of water may be said to be the following:

For land:

Conductivities - from 1·10^-14 to 100·10^-14 electromagnetic unit

for land of various kinds Inductivities - (ordinary dielectric constant) from 2 to 25, depending

upon the amount of water in the soil

For fresh water:

Conductivities of the order of 10·10^-14 electromagnetic unit. Inductivity about 81.

For typical ocean water:

Conductivity of about 5,000·10^-14 electromagnetic unit. Inductivity about 81

The above values are expressed in electromagnetic units because most available propagation data are prepared in these units for engineering use. The procedure of using the factor 10^-14 permits the relative conductivity to be immediately apparent from reading the value of the coefficient, the value 1·10^-14 being low enough to include almost the poorest kind of soil that would be encountered. Values of conductivity lower than this are equivalent values for attenuation conditions due not only to the soil characteristics but to losses due to wave scattering. Therefore it may be found that in topographically rugged country it appears that the average conductivity is below 1·10^-14, whereas the earth itself, if flat, would in almost all cases be above this value. The additional attenuation of a wave due principally to scattering by reflections from the irregular terrain is then equivalent to that over a flat earth with much lower conductivity.

When a plane electromagnetic wave with its electric field normal to the direction of propagation impinges upon the surface of an imperfect dielectric, the power propagated into the dielectric sets up conduction currents and displacement currents, both in quadrature to each other. The ratio of the two is dependent upon the frequency, the conductivity, and the inductivity. At the lowest radio frequencies, conduction currents are very large with respect to the displacement currents, permitting the latter to be neglected. With increasing frequency, displacement currents become more important relatively, and eventually a frequency is reached where displacement currents predominate over conduction currents.

Conduction-current density is maximum at the surface of the ground and decreases exponentially with depth. The depth at which the magnitude of the current density has fallen to 1/e of its surface value (about 37 percent. is called the "skin depth" which we shall designate by the letter S. The conduction-current skin depth in meters can be computed from the relation where σ is in electromagnetic units and f in cycles per second.

Appendix II shows the skin depths for the range of frequencies and, soil conductivities of general interest. The skin depth equals one-half wavelength at the velocity of propagation in the soil and about 90 percent of all the loss in the soil occurs within this depth.

The earth currents return to the base of a vertical antenna along radial lines. At the base of the antenna, all the ground currents add together to enter the antenna as the antenna current. The total ground loss is the integrated losses at all points due to all the returning ground currents. In ordinary soils this loss is considerable, and measures have to be taken to minimize ground loss by the use of systems of buried radial wires that conduct the returning ground currents to the base of the antenna through high-conductivity circuits.

The distance from the antenna at which returning ground currents are of such a low value as to be negligible is of the order of 0.5 wavelength. Beyond about 0.4 wavelength, the gain in efficiency with increased length is seldom a good economic investment, when a sufficiently large number of radials is used. Systematic measurements6 have shown that the effective length of a buried wire decreases as the number of radial wires is decreased. Ground resistance decreases as both the length and the number of buried radial wires are increased. However, when the number of radials exceeds 120 and their length exceeds 0.4 wavelength, one reaches the region of diminishing returns. With such a ground system, the circuital and radiational characteristics of a vertical radiator of the type used for broadcasting approach very nearly those computed from theory for a perfectly conducting earth. Figure 2.17 shows how the field strength varies as a function of antenna height and the number of 0.412-wave-length radial ground wires. Figure 2.18 shows the same thing, but with 0.137-wavelength radials. Figure 2.19 shows the field strength and the antenna resistance of a 77-degree radiator as a function of the number of 0.412-wavelength radials used. These data were obtained from experimental studies at 3,000 kilocycles.6

The ground system performs solely as a circuital element with the shorter vertical radiators, serving to reduce ground losses. With a system of 120 radial wires buried near the surface of the soil to a length of 0.4 to 0.5 wavelength, almost all of the ground current is collected from the electric field above the ground system and current densities below the ground system are very small. Currents in the soil between the radials are quickly diffracted into the wires.

With high radiators of the antifading type, however, the ground system performs another function - that of providing a reflecting surface of high reflectivity for those electromagnetic fields which produce cancellation of high-angle radiation. Surface-reflection losses cause incomplete wave interference because the reflected field strength is decreased in amplitude by these losses.

From the principles of the reflection of a plane electromagnetic wave from the boundary between air and an imperfect dielectric of conductivity σ and inductivity ε at a frequency / in cycles, the reflection coefficient Kν for vertically polarized waves is the following vector (Fresnel) equation:

in which a is the angle above the horizon and is the complement of the angle of incidence. This is the Fresnel equation for vitreous reflection, and the value of σ in this equation is in centimeter-gram-second electrostatic units. To convert from customary electromagnetic units to electrostatic units, use the relation

It is evident from this equation that the complex reflection coefficient is a function of the conductivity and the inductivity of the ground, the frequency, and the angle of elevation above the ground. This means that there is always a decrease in the magnitude of the reflected wave with respect to the incident wave, and there is a change of phase ψν as well.

FIG. 2.17. Field strength as a function of antenna height and the number of 0.412-wavelength radial ground wires, 1,000 watts antenna input. (After Brown, Lewis, and Epstein)

FIG. 2.18. Field strength as a function of antenna height and the number of 0.137-wavelength radial ground wires, 1,000 watts antenna input. (After Brown, Lewis, and Epstein)

When the computation is made for the values of Kν as α varies from 0 to 90 degrees, it will be found that at some angle αb the amplitude |K| is a minimum, and at this elevation the value of ψ is - 90 degrees. The elevation angle α_b is known as the "pseudo-Brewster angle." If the ground were a perfect isotropic dielectric ( σ = 0), it would be found that |K| = 0 at the Brewster angle.

FIG. 2.19. Field strength for a 77-degree vertical radiator as a function of the number of 0.412-wavelength radial ground wires, 1,000 watts antenna input. (After Brown, Lewis, and Epstein.)

The significance of these facts is that a vertical radiation pattern at a very great distance differs from that which is computed without taking into account the imperfect conductivity and the inductivity of the ground. Up to this point all discussion of vertical radiation patterns has followed the assumption that the ground was of perfect conductivity. The construction of an optimum practical ground system for a vertical radiator tends to approach this ideal condition from a circuital standpoint and for wave reflections that occur within the radius of the ground system. For waves reflected from the surface beyond the limits of the ground system, the actual ground constants may impose a substantial change in the vertical radiation pattern at the low angles, by modifying both its amplitude and its shape.

Table 2.6 will provide a general idea of the importance of these facts for two values of conductivity when the frequency is 1 megacycle.