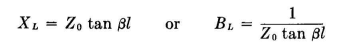Parallel Stub Lines for Impedance Matching

Author: Edmund A. Laport

In this method, the Q of the line is measured as in previous techniques, and a current minimum is located. The problem is to find a point on the line where the real component G of its admittance Y = G ± jB is equal to the characteristic admittance Y₀ of the main feeder. At this point, a short stub of line, either open-circuited or short-circuited at its outer end, is bridged across the line. The susceptance of the stub is made equal but of opposite sign to the susceptance of the feeder at the point of attachment.

The circle diagram (Fig. 4.58) may also be read in terms of conductance and susceptance in the same way it was previously used for resistance and reactance, reading conductance in mhos instead of resistance in ohms and susceptance in mhos instead of reactance in ohms.

A stub line that is short-circuited is more easily adjusted than one open-circuited, and is for that reason the commonly preferred type. When its length βl < 90 degrees, the stub is inductively reactive and therefore has positive susceptance. A point on the feeder can always be found where the susceptance is negative and therefore requires a stub of positive susceptance to neutralize it.

FIG. 4.38. Location and reactance of an impedance-matching shunt coil, derived from Fig. 3.58.

Such a stub is designed from the equations

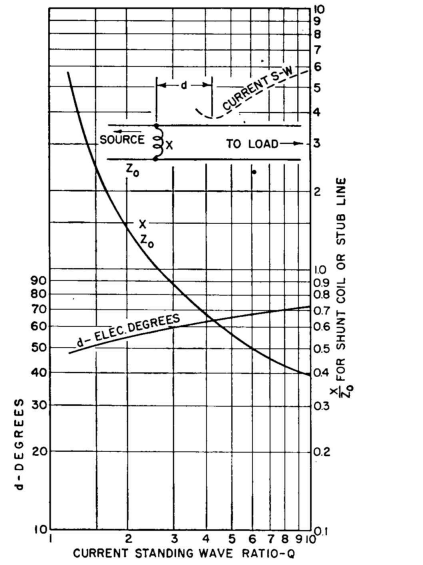
When the stub line has the same characteristic impedance as the feeder, Fig. 4.37 can be used to read directly the location and length of both open-circuited and short-circuited stubs for a correct impedance match.