Type III Problem

Author: Edmund A. Laport

Problem. What elements are required for a phase-shifting network which will introduce a phase shift of -120 degrees in a circuit having a characteristic impedance that is 100 ohms resistive?

Fig. 5.24

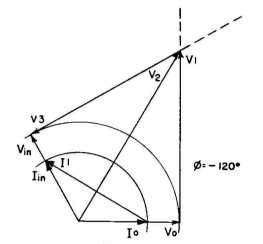
Procedure. Write the problem vectorially as shown in Fig. 5.25. Because input impedance equals the load impedance, the input is represented by vectors of the same length as for the load, but with the specified phase difference. Then, if we chose a T network (Fig. 5.26), we erect perpendiculars through V₀ and V_in and connect I₀ with I_in as shown in Fig. 5.27. From this we obtain the solution shown in Fig. 5.28.

Fig. 5.25

Fig. 5.26

Had we chosen the π solution, the vector diagram would have been as shown in Fig. 5.29.

A reversal of the phase angle in any problem reverses the signs of all the elements. For instance, in this problem, if the phase angle had been + 120 degrees, all elements would change from L to C, and vice versa, maintaining the same numerical values.

A phase-shifting network of this type is equivalent to a section of an infinite transmission line having a characteristic impedance R₀ and an electrical length equal to that of the angle of phase shift, which in such cases must be negative. This provides a handy device to study certain properties of lines, such as the 45 degree and the 90 degree sections which have special properties.

Fig. 5.27

Fig. 5.28

Fig. 5.29

For example, how does the input impedance of a 45 degree section of a transmission line change with variation of the terminal resistance from 0 to ? Solve for the equivalent single-stage network having a characteristic impedance R₀ when it is terminated in a resistance R₀ by assuming it to be a -45 degree phase-shifting network. (We illustrate with the T network.) The vector diagram is shown in Fig. 5.30. Thus, taking R₀ as unity, we obtain the ratio of all other elements to R₀ . We can then assume any value of terminal resistance and calculate the resulting input impedance. We obtain the circuit of Fig. 5.31.

The limiting conditions are quickly examined by assuming open-circuit and short-circuit terminal conditions. For the former, Z_in is the sum of j0.42 and -j1.42, which is -j1.00. For the latter, the solution for Z_in yields +j1.00. So we easily find that Z_in remains constant in magnitude for all conditions of resistance termination but varies in character from pure capacitive reactance, through pure resistance to pure inductive reactance as the terminal resistance varies from to 0.

Fig. 5.30

Proceeding in the same manner, the 90-degree network is analyzed.

´Fig. 5.31 unbeschrifte

Its special property of impedance inversion is worthy of digression to see why it works as it does. The vector diagram for a -90-degree T network with a characteristic impedance R₀ is given in Fig. 5.32. From this we find the equivalent circuit elements, in terms of R₀ , to be those of Fig. 5.33.

All the elements of the network have reactances equal in magnitude to R₀ .

FIg 5.32

At this point we can test the circuit for open- and short-circuit terminal conditions and see what happens to Z_in. When R_t = R₀ , Z_in = R₀ . When R_t = 0, X₁ and X₂ in parallel give a condition of anti-resonance and Z_in = . When R_t = , X₂ and X₃ in series tune to series resonance, making Z_in = 0.

Fig. 5.33

Thus the boundary conditions of impedance inversion in a 90-degree network or transmission-line section are demonstrated.