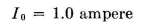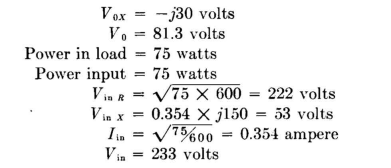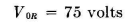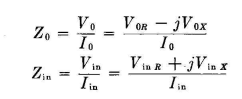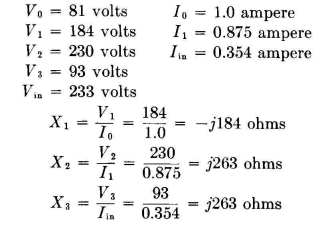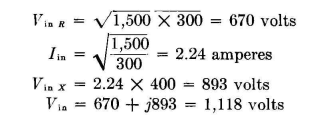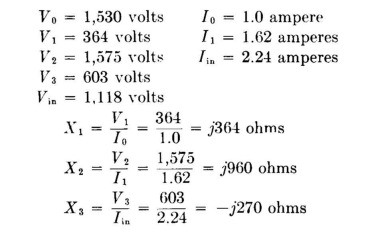Type II Problem

Author: Edmund A. Laport

Problem. We desire to couple a load circuit having an impedance of Z₀ = 75 - j30 to a circuit which requires a terminating impedance of Z_in = 600 + j150. The transformation, let us say, must be made with a phase difference between the load current and the input current of plus 60 degrees. What is the network design required?

Procedure. The problem is set up in vector form first, on the basis that power input equals power output.

Let

Then

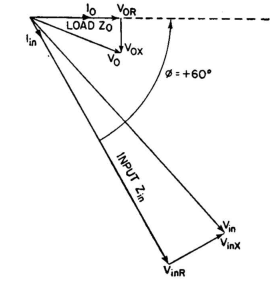
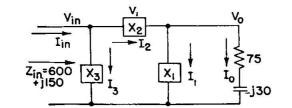
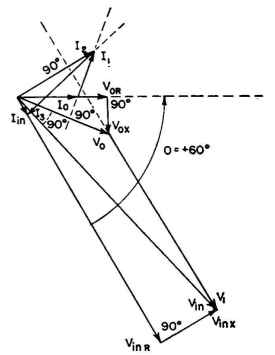
To solve for the network required to make the indicated transformation, complete the vector diagram as shown in Fig. 5.14, and obtain therefrom the nature and magnitude of the required reactances.

Fig. 5.14

There is a choice between a π and T network, Let us illustrate by using a T network.

Fig. 5.15

Draw the circuit, and label all potentials and currents, as in Fig. 5.15.

Draw V₁ in a direction perpendicular to I₀, starting at V₀, as shown in

Fig. 5.16. Then draw V₃ in a direction perpendicular to Iin, through Vin. The intersection of these perpendiculars locates the lengths of V₁, V₂, and V₃. Draw V₂ from the origin to the intersection.

Fig. 5.16

As a check on accuracy, measure the angle between I₁ and F₂ - it should be 90 degrees.

Fig. 5.17

As before, I₁ is drawn to connect I₀ and Iin. From the scales of Fig. 5.15

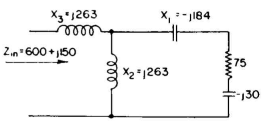
The network becomes that shown in Fig. 5.17.

Solving this same problem on the basis of a π network (Fig. 5.18), we construct Fig. 5.19. Tabulating values from vector scales, we obtain

The circuit becomes that of Fig. 5.20.

Fig. 5.18

Fig. 5.19

Fig. 5.20

Problem. Calculate the required elements of a network which will make a transformation from 1,500 + j300 (load) to 300 - j400, so that the potential across the load is in phase with the input potential.

Procedure. Vector statement of this problem is, after resolving the input and load potentials into their resistive and reactive components on the basis of equality of power at input and output, shown in Fig. 5.21 with the scales chosen (for example, 1 inch = 1.0 ampere and 1 inch = 500 volts).

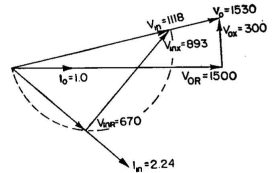
This shows V_in in phase with V₀ as required, and the relative directions of I₀ and I_in. It also is marked to show the potentials and currents prevailing in the load and for the input to the network. From this point, the vector diagram must be completed for either a π or a T network. We shall demonstrate both and compare them.

Fig. 5.21

The block diagram of the π network version for this problem is shown in Fig. 5.22. The vector diagram shows that V₀ and V_in are in phase. Vectors I₁ and I₃ must both be perpendicular to the direction of V₀ and Vin; thus they can never intersect. A solution with a π network is therefore impossible.

Fig. 5.22

Fig. 5.23

The T network provides a solution for the problem as shown in Fig. 5.23.

The network is shown in Fig. 5.24.

NOTE: If the problem had specified that the load and input currents be in phase, then a π solution would be possible and the T solution impossible.