You are working with the text-only light edition of "H.Lohninger: Teach/Me Data Analysis, Springer-Verlag, Berlin-New York-Tokyo, 1999. ISBN 3-540-14743-8". Click here for further information.
| You are working with the text-only light edition of "H.Lohninger: Teach/Me Data Analysis, Springer-Verlag, Berlin-New York-Tokyo, 1999. ISBN 3-540-14743-8". Click here for further information.
|
Table of Contents  Univariate Data Measures of Variation Coefficient of Variation |
|
| See also: standard deviation, Signal and Noise |   |
Specifying the standard deviation
is more or less useless without the additional specification of the mean
value (and of course the type of distribution). It makes a big difference
if s = 5 with a mean of 
= 100, with a mean of
= 3. Relating the standard deviation to the mean resolves this problem.
The coefficient of variation is therefore defined by
,
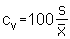which is a relative measure of the variation. However you should be aware of the fact that the coefficient of variation becomes more or less useless when the mean approaches zero. So don't use the coefficient of variation for comparing detection limits (where the signal to noise ratio falls below 3).
Last Update: 2006-Jän-17