You are working with the text-only light edition of "H.Lohninger: Teach/Me Data Analysis, Springer-Verlag, Berlin-New York-Tokyo, 1999. ISBN 3-540-14743-8". Click here for further information.

Index
See also: introduction to convolution 

Convolution
Mathematical Details

There is a German word for convolution, Faltung ("folding"), which aptly expresses the process involved in convolution. Two signals g(t) and h(t) are convolved ("folded") by multiplying the two signals and summing the product terms. Thus the convolution result for any given parameter t is defined as

,
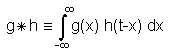
with 2n being the maximum of the number of samples of either signals. This sum of products is called the discrete convolution. There is also a continuous definition of the convolution:
The convolution is closely linked with the Fourier transform and to the correlation function. The "Convolution Theorem" says that the Fourier transform of the convolution is the product of the individual Fourier transforms:

g * h = G(f)H(f)

The correlation of two signals, which is defined as

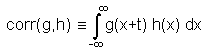
can also be expressed as a product of two individual Fourier transforms:

corr(g,h) = G(f)H(-f)


 














Last Update: 2002-Nov-03