You are working with the text-only light edition of "H.Lohninger: Teach/Me Data Analysis, Springer-Verlag, Berlin-New York-Tokyo, 1999. ISBN 3-540-14743-8". Click here for further information.
| You are working with the text-only light edition of "H.Lohninger: Teach/Me Data Analysis, Springer-Verlag, Berlin-New York-Tokyo, 1999. ISBN 3-540-14743-8". Click here for further information.
|
Table of Contents  Univariate Data Sampling Distributions F Distribution |
|
| See also: sampling distributions, chi-square distribution, t-distribution |   |
The F-distribution becomes relevant when we try to calculate the ratios of variances of normally distributed statistics. Suppose we have two samples with n1 and n2 observations, the ratio
is distributed according to an F distribution (named after R.A. Fisher) with df1 = n1-1 numerator degrees of freedom, and df2 = n2-1 denominator degrees of freedom. The F-distribution is skewed to the right, and the F-values can be only positive.
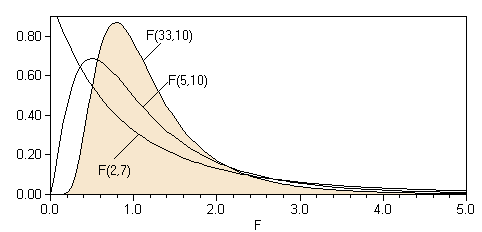
Note that three of the most important distributions (namely the normal
distribution, the t distribution, and the chi-square distribution) may
be seen as special cases of the F distribution:
| normal distribution | = F(1,infinite) |
| t distribution | = F(1, n2) |
| chi-square distribution | = F(n1, infinite) |
Last Update: 2005-Jul-16