You are working with the text-only light edition of "H.Lohninger: Teach/Me Data Analysis, Springer-Verlag, Berlin-New York-Tokyo, 1999. ISBN 3-540-14743-8". Click here for further information.

	Index
See also: Fourier transformation, FFT

Fourier Series

Any periodic signal y(t) may be constructed from a infinite sum of sine and cosine terms:

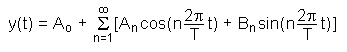
with A_i and B_i being the Fourier coefficients, and T the duration of the period of the function y(t). The coefficient A₀ represents the aperiodic fraction of the signal (i.e. A₀ is equal to the average amplitude of the signal). The terms for each frequency may be rearranged to form a single cosine term with the magnitude  and the phase angle phi_n = tan^-1 (B_n/A_n).

The set of cosine and sine functions is complete and orthogonal, which guarantees that any periodic function f(t) can be represented, and that the Fourier coefficients are independent of each other.

The following interactive example shows you how to combine sines and cosines to form a signal y(t). By setting the coefficients A_i and B_i one can immediately see their effect on the resulting function.

Last Update: 2004-Jul-03