You are working with the text-only light edition of "H.Lohninger: Teach/Me Data Analysis, Springer-Verlag, Berlin-New York-Tokyo, 1999. ISBN 3-540-14743-8". Click here for further information.

Table of Contents Math Background Matrices Matrix Determinants - Calculation of Order 2 and 3	Index
See also: matrix determinant, rank of a matrix

Matrix Determinants
Calculation of Order 2 and 3

The general approach how to calculate a matrix determinant is hard, requiring the calculation of many similar steps. Thus it is not recommended to calculate a determinant of matrices with an order higher than 3 without the help of a computer. For matrices of order 2 and 3 there are special rules which make it comparatively easy to determine the determinant:

Determinant of matrices of order 2

Let

a11 a21

a12 a22

be an arbitrary matrix of order 2. Then its determinant is calculated as the product of the principal diagonal minus the product of the other diagonal, formally a₁₁a₂₂ - a₁₂a₂₁.

Determinant of matrices of order 3 (Sarrus' Rule)

Let

a11 a21 a31

a12 a22 a32

a13 a23 a33

be an arbitrary matrix of order 3. Then its determinant is calculated as the sum of the product of all "extended" falling (including the principal) diagonals minus the sum of the product of all "extended" rising diagonals, formally (a₁₁a₂₂a₃₃ + a₂₁a₃₂a₁₃ + a₃₁a₁₂a₂₃) - (a₃₁a₂₂a₁₃ + a₂₁a₁₂a₃₃ + a₁₁a₃₂a₂₃). This rule is easier to understand when we color the relevant diagonals:

Example: determinant of a matrix of order 3

Let

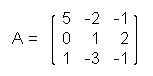
Then

Last Update: 2006-Jän-17