You are working with the text-only light edition of "H.Lohninger: Teach/Me Data Analysis, Springer-Verlag, Berlin-New York-Tokyo, 1999. ISBN 3-540-14743-8". Click here for further information.

Table of Contents Math Background Matrices Matrix Inversion	Index
See also: identity matrix, pseudo-inverse matrix

Matrix Inversion

Matrix inversion plays a major role in many multivariate techniques. While the inverse of a matrix is defined only for quadratic matrices, the concept of matrix inversion can also be extended to rectangular matrices by introducing the pseudo-inverse of a matrix.
 
 

Inverse Matrix

Given a square matrix A, the inverse matrix X is defined by the following equation: AX = IThe inverse of A is denoted by A-1 and is unique. Note that not all square matrices can be inverted. If an inverse for A exists, Ais called a regular or nonsingular matrix, otherwise A is a singular matrix. For regular matrices, the following equation is valid: AA-1 = A-1A = I.

Please note that (AB)^-1 is not equal to A^-1B^-1, but rather to B^-1A^-1. The inverse of a matrix may be calculated using several algorithms, one of them being the Gauss Jordan algorithm.
 

Example: Inverse Matrix

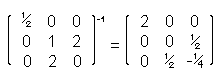
since 

 

 

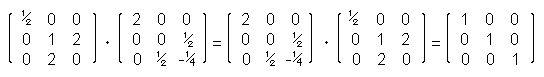
Last Update: 2005-Jän-25