 You are working with the text-only light edition of "H.Lohninger: Teach/Me Data Analysis, Springer-Verlag, Berlin-New York-Tokyo, 1999. ISBN 3-540-14743-8". Click here for further information.
You are working with the text-only light edition of "H.Lohninger: Teach/Me Data Analysis, Springer-Verlag, Berlin-New York-Tokyo, 1999. ISBN 3-540-14743-8". Click here for further information.
 You are working with the text-only light edition of "H.Lohninger: Teach/Me Data Analysis, Springer-Verlag, Berlin-New York-Tokyo, 1999. ISBN 3-540-14743-8". Click here for further information. You are working with the text-only light edition of "H.Lohninger: Teach/Me Data Analysis, Springer-Verlag, Berlin-New York-Tokyo, 1999. ISBN 3-540-14743-8". Click here for further information.
|
Table of Contents  Math Background Math Background  Introduction to Probability Introduction to Probability  Bayesian Rule Bayesian Rule |
|
| See also: conditional probability |   |
The Bayesian rule, as developed below, enables us to compute the probability of an event by first determining whether or not some other event has occurred. In some situations, it is easier to compute the probability of an event as soon as we know if some other event has occurred.
Given the events A and B, we can express A = (A Ç
B) È (A Ç
B'):
 Ç
Ç |
È |  Ç
Ç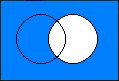 |
= |
| ( A Ç B ) | È | ( A Ç B' ) | = |
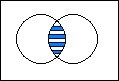 |
È |
 |
= |
 |
| A |
Since (A Ç B) and (A Ç B') are mutually exclusive, their probabilities can simply be added to obtain the probability of P(A):
P(A) = P (A Ç B) + P(A Ç
B') = P(A|B) . P(B) + P(A|B') . P(B')
P(A) = P(A|B) . P(B) + P(A|B') . [1-P(B)]
The probability of the event A is the weighted average of the conditional
probabilities of A given B, and A given not B. The weights for the conditional
probabilities are defined by the probabilities of the conditional events
B and not B.

P(E) is the weighted average of P(E|Fi), the weight being the probability of the event Fi on which it is conditioned.

When we interpret the Fj as hypotheses about a question,
Bayes' formula shows us how the evidence should change our opinion held
prior to the experiments.
Last Update: 2005-Jšn-25