Teach/Me Data Analysis

You are working with the text-only light edition of "H.Lohninger: Teach/Me Data Analysis, Springer-Verlag, Berlin-New York-Tokyo, 1999. ISBN 3-540-14743-8". Click here for further information.

	Index
See also: conditional probabilities

Independent Events

A and B are independent events if the occurrence of B does not influence the probability that A occurs, and vice versa:

P(A|B) = P(A)
and
P(B|A) = P(B).

Experiments are usually (or should be) planned such that they are independent.

Example:

A coin is tossed twice and we define the events A{the 1^st toss is a head} and B{the 2^nd toss is a head}. Does the result of the first toss affect the result of the second toss? Intuitively, we would say 'No', but we want to prove it.
P(A) = P(HH) + P(HT) = ½ , P(B) = P(TH) + P(HH) = ½.
P(B|A) = P(A Ç B) / P(A) = P(HH) / P(A) = ¼ / ½ = ½
We see that P(B|A) = P(B), i.e. the event A has no influence on the outcome of B. The events are independent of each other.

NOTE

Independence is a difficult concept and cannot be shown in a diagram. It is not intuitive and one has to check it for each situation.
The probability of the intersection of independent events is the product of the probabilities of the events.

When A and B are independent, then A and B' are independent, too.
Two mutually exclusive events A and B are dependent! If B has occurred, it is impossible for A to occur simultaneously.
When A is independent of B and A is independent of C, A is not necessarily independent of (B Ç C).

Independence of several events

When

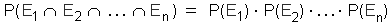, then all sub-events E_i are independent, too. A set of events is independent if every finite subset of these events is independent, too. Sometimes the probability of an experiment consists of a series of sub-experiments (tossing coins several times, one toss). In many cases we can assume that outcomes are independent. If all the experiments are identical and if the experiments have the same sample space and probability, we speak of trials.

Last Update: 2004-Jul-03