 You are working with the text-only light edition of "H.Lohninger: Teach/Me Data Analysis, Springer-Verlag, Berlin-New York-Tokyo, 1999. ISBN 3-540-14743-8". Click here for further information.
You are working with the text-only light edition of "H.Lohninger: Teach/Me Data Analysis, Springer-Verlag, Berlin-New York-Tokyo, 1999. ISBN 3-540-14743-8". Click here for further information.
 You are working with the text-only light edition of "H.Lohninger: Teach/Me Data Analysis, Springer-Verlag, Berlin-New York-Tokyo, 1999. ISBN 3-540-14743-8". Click here for further information. You are working with the text-only light edition of "H.Lohninger: Teach/Me Data Analysis, Springer-Verlag, Berlin-New York-Tokyo, 1999. ISBN 3-540-14743-8". Click here for further information.
|
Table of Contents  Introductory Stuff Introductory Stuff  Definition of basic terms Definition of basic terms  Random Experiment Random Experiment |
|
| See also: random variable, random number |   |
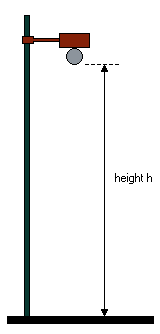 Let's
have a look at a fairly simple, precisely defined experiment, which was
originally performed to investigate the laws of gravitation. A steel ball
is mounted at some known fixed height above ground within an evacuated
apparatus. When the steel ball is released, the time until it hits the
ground plate is measured. Suppose the steel ball is mounted at a height
of exactly 5 meters above ground. Using an electronic stopwatch with a
time resolution of 0.001 sec, we would determine that the steel ball needs
1.010 seconds to hit the ground. Now let's repeat the experiment. Again,
the steel ball needs 1.010 seconds to hit the ground. Repeating the experiment
10 times, we find the following free fall durations (in seconds):
Let's
have a look at a fairly simple, precisely defined experiment, which was
originally performed to investigate the laws of gravitation. A steel ball
is mounted at some known fixed height above ground within an evacuated
apparatus. When the steel ball is released, the time until it hits the
ground plate is measured. Suppose the steel ball is mounted at a height
of exactly 5 meters above ground. Using an electronic stopwatch with a
time resolution of 0.001 sec, we would determine that the steel ball needs
1.010 seconds to hit the ground. Now let's repeat the experiment. Again,
the steel ball needs 1.010 seconds to hit the ground. Repeating the experiment
10 times, we find the following free fall durations (in seconds):
1.010, 1.010, 1.010, 1.010, 1.010, 1.010, 1.010, 1.010, 1.010, 1.010
Now let's conduct the same investigation once again, but replace the
electronic stopwatch with a device which has a 10 million fold time resolution
(nsec instead of msec). Repeating the experiment 10 more times, we now
find the following values for the duration of the free fall:
1.009810350, 1.009810943, 1.009810257, 1.009810072, 1.009810929,
1.009810704, 1.009810009, 1.009810542, 1.009812001, 1.009800763
Looking at the outcome of the second set-up, we see that the results
are exact only to a certain precision. Increasing the precision of the
experiment finally reveals some fluctuations in the results which seam
to be completely random. When we use some kind of "magnification
glass" to look at the results, we finally find that the outcome varies
from time to time. You may go to the ![]() to have a look at the data.
to have a look at the data.
The result of this experiment can be seen in more fundamental way:
Any experiment producing an analog signal will finally show up random numbers if we only measure the results precisely enough.
Last Update: 2006-Jšn-17