 You are working with the text-only light edition of "H.Lohninger: Teach/Me Data Analysis, Springer-Verlag, Berlin-New York-Tokyo, 1999. ISBN 3-540-14743-8". Click here for further information.
You are working with the text-only light edition of "H.Lohninger: Teach/Me Data Analysis, Springer-Verlag, Berlin-New York-Tokyo, 1999. ISBN 3-540-14743-8". Click here for further information.
 You are working with the text-only light edition of "H.Lohninger: Teach/Me Data Analysis, Springer-Verlag, Berlin-New York-Tokyo, 1999. ISBN 3-540-14743-8". Click here for further information. You are working with the text-only light edition of "H.Lohninger: Teach/Me Data Analysis, Springer-Verlag, Berlin-New York-Tokyo, 1999. ISBN 3-540-14743-8". Click here for further information.
|
Table of Contents  Bivariate Data Bivariate Data  Regression Regression  Confidence Intervals Confidence Intervals |
|
| See also: regression, derivation of regression formula |   |
When calculating a regression line, one estimates the mean of the population
of Y at any value of X. Thus the regression line represents the mean 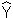 i
at any value of the independent variable X. This estimated mean is normally
distributed, and one may ask the question about the confidence interval
of the estimated Y. It can be shown that the ratio (
i
at any value of the independent variable X. This estimated mean is normally
distributed, and one may ask the question about the confidence interval
of the estimated Y. It can be shown that the ratio (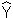 - my)/s2 follows
a t-distribution with n-2 degrees
of freedom. From this, one can calculate the confidence interval of the
estimated Y by the following equation
- my)/s2 follows
a t-distribution with n-2 degrees
of freedom. From this, one can calculate the confidence interval of the
estimated Y by the following equation
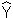
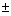 s2 tn-2
s2 tn-2
 |
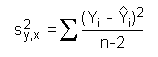 |
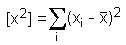 |
If you are plotting the confidence interval for the population regression line, you see that these lines are hyperbolic. This means that the confidence interval depends on the value of X. The farther the value of X departs from 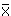 , the larger is the confidence interval (inner, blue curve of figure below). The band formed by the confidence interval for all X values is also called Working-Hotelling confidence band.
, the larger is the confidence interval (inner, blue curve of figure below). The band formed by the confidence interval for all X values is also called Working-Hotelling confidence band.
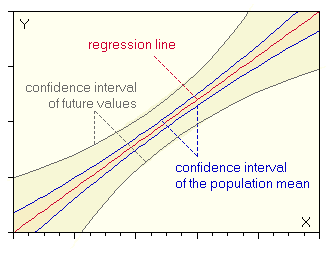
In practical situations the confidence interval of the population mean
is not so frequently required, while most of the inferences are based upon
the estimation of a distinct, future 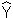 i,
which is not known at the time when the regression is calculated and which
is independent from any previous values. The confidence interval for future
observations is given by the following equation:
i,
which is not known at the time when the regression is calculated and which
is independent from any previous values. The confidence interval for future
observations is given by the following equation:
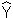
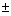 s3 tn-2
s3 tn-2
 |
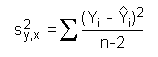 |
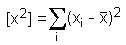 |
The confidence interval for actual (future) values of Y is wider than
the confidence interval for the population mean (outer, gray curve in figure
above). This demonstrates the fact that the estimate of the actual value
of Y is less precise than the estimate of the mean of Y.
Last Update: 2005-Jul-16