You are working with the text-only light edition of "H.Lohninger: Teach/Me Data Analysis, Springer-Verlag, Berlin-New York-Tokyo, 1999. ISBN 3-540-14743-8". Click here for further information.
| You are working with the text-only light edition of "H.Lohninger: Teach/Me Data Analysis, Springer-Verlag, Berlin-New York-Tokyo, 1999. ISBN 3-540-14743-8". Click here for further information.
|
Table of Contents  Bivariate Data Regression Introduction |
|
| See also: regression of a straight line, history, multiple linear regression, ANOVA |   |
A common situation in data analysis is that someone has acquired data on unknown samples, which shows a relationship between the measured variables. For example, one could have measured the number of cars per hour passing a tunnel in the Alps, and the carbon monoxide and the benzene concentration in the tunnel air. These variables are related to each other. For quantifying the relationship one has to set up a model which relates the number of cars to the benzene concentration.
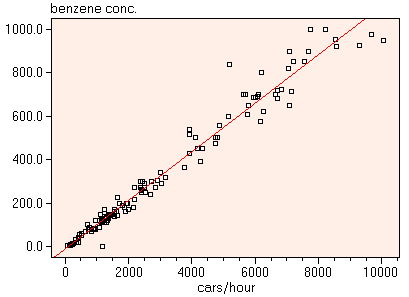
In the most simple case, the model to be determined is a straight line. However we could use the same methods of regression to fit other types of models as well (as long as the models stay linear).
One common problem with the classical regression models is that outliers
have much influence on the overall result of the regression. You may take
a quick look at this effect by using this 
.
This effect is called leverage effect.
Last Update: 2005-Jul-16