You are working with the text-only light edition of "H.Lohninger: Teach/Me Data Analysis, Springer-Verlag, Berlin-New York-Tokyo, 1999. ISBN 3-540-14743-8". Click here for further information.

Table of Contents Statistical Tests Means One Sample t-Test Large Sample Size
Index
See also: survey on statistical tests, small samples, two-sample t-test, distribution calculator 

One-Sample t-Test
Large Samples



Let's assume that we have to fill containers with an expensive substance. Our customers expect a guaranteed quantity m of the material. We know the precision s of our machinery and want to check whether we have adjusted our dispenser correctly. Since measurements are rather cheap (i.e. we only have to weigh the container) we can afford a lot of measurements n. The question we have to answer is how large does the mean quantity have to be, so that we don't have to reject the assumption that our filling procedure is correct. Since we have to acknowledge the possibility of an erroneous decision, we are content when our error probability is smaller than a %. The probability a is called the confidence level.

The decision can be made according to the table below:


1. We have to formulate our two hypotheses (the null hypothesis H0 and the alternative hypothesis H1): 

H0: amount <= limit
H1: amount >  limit
2. Next, we specify a level of significance (or confidence level) which meets our requirements (a common confidence level is 5 %).

3. In order to decide which of the two hypotheses is true we calculate the test statistic

,

which is normally distributed. The z value gives us the distance of the measured  from the specified value µ in terms of the standard deviation s, e.g. when z=1.5, the distance is 1.5 s.

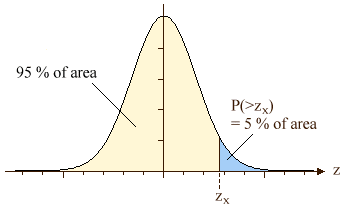
4. Defining the region of rejection. In order to know when we have to reject the null hypothesis (i.e.  is less than m) we have to define the rejection region by specifying the critical value of z. The rejection region depends on the level of significance. The critical z value is that particular value on the x-axis of the distribution function for which the area under the distribution function to its right is exactly a percent. We can find this value from a z table: zx = z(0.95) =1.645; or you may start the Teach/Me distribution calculator to calculate the value of interest.

Figure 3c

5. Finally, we have to select the appropriate hypothesis by inserting the numerical values for , µ, s and n into the equation for z. We do not reject the null hypothesis (note the subtle difference to "we accept the null hypothesis") if the calculated z value is smaller than zx = 1.645.
 

Note: A more general approach is to use the t-distribution for testing, since the t-distribution approaches the normal distribution for large sample sizes.

Last Update: 2005-Jul-16