You are working with the text-only light edition of "H.Lohninger: Teach/Me Data Analysis, Springer-Verlag, Berlin-New York-Tokyo, 1999. ISBN 3-540-14743-8". Click here for further information.

Index
See also: model finding, establishing ARIMA models 

Time Series
Definition of ARIMA Models

ARIMA (auto-regressive integrated moving average) models establish a powerful class of models which can be applied to many real time series. ARIMA models are based on three parts: (1) an autoregressive part, (2) a contribution from a moving average, and (3) a part involving the first derivative of the time series:

The auto-regressive part (AR) of the model has its origin in the theory that individual values of time series can be described by linear models based  on preceding observations. For instance: x(t) = 3 x(t-1) - 4 x(t-2). The general formula for describing AR[p]-models (auto-regressive models) is:

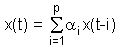
The order of the model is determined by p.

The consideration leading to moving average models (MA models) is that time series values can be expressed as being dependent on the preceding estimation errors. Past estimation or forecasting errors are taken into account when estimating the next time series value. The difference between the estimation x(t) and the actually observed value x(t) is denoted e(t). For instance: x(t) = 3 e(t-1) - 4 e(t-2).

The general description of MA[q]-models is:

When combining both AR and MA models, ARMA models are obtained. In general, forecasting with an ARMA[p,q]-model is described using the following equation:

After additional differentiation of the time series, and integrating it after application of the model, one speaks of ARIMA models. They are used when trend filtering is required. The parameter d of the ARIMA[p,d,q]-model determines the number of differentiation steps.
 

    First, the time series is derived d times until it is stationary.
    Then, a suitable ARMA[p,q] model is fitted to the resulting series.
    Finally, the estimated forecasts have to be integrated d times.
Many more variants of ARIMA models have been introduced to treat specific cases. Here, the whole group of such models is subsumed under the term ARIMA models. Since their characteristics are determined by the three parameters p, d, and q, they are also referred to as ARIMA[p,d,q]-models. The parameter p denotes the order of the auto-regressive part, the parameter q the order of the moving average part, and d the number of differentiation steps.
 

Last Update: 2004-Jul-03