You are working with the text-only light edition of "H.Lohninger: Teach/Me Data Analysis, Springer-Verlag, Berlin-New York-Tokyo, 1999. ISBN 3-540-14743-8". Click here for further information.
| You are working with the text-only light edition of "H.Lohninger: Teach/Me Data Analysis, Springer-Verlag, Berlin-New York-Tokyo, 1999. ISBN 3-540-14743-8". Click here for further information.
|
| See also: forecasting |   |
When measuring the temperature twice a day, the resulting time series may be as follows:
Two typical phenomena can be observed: an upward trend and daily cycles. Both the trend and seasonal patterns have to be removed before any model can be established, because typical models require stationary time series. When the characteristics of a time series (for instance, the mean and the variance) differ at different points in time, the time series is non-stationary. After removing the trend of the time series in our example, the time series looks like this:
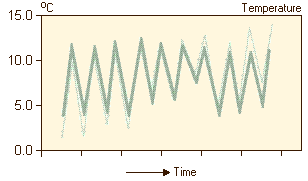
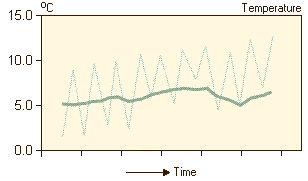
After averaging out the daily cycles, which are caused by measuring twice a day, the following time series is obtained:
Finally, removing both the trend and the cycles results in the following series:
Now, it is time to check the properties of the resulting time series.
If it is actually stationary, it provides the basis for setting up a model.
In order to forecast future values, the result obtained by using the model
has to be transformed so that the trend and the daily cycle are again taken
into account.
Last Update: 2004-Jul-03