You are working with the text-only light edition of "H.Lohninger: Teach/Me Data Analysis, Springer-Verlag, Berlin-New York-Tokyo, 1999. ISBN 3-540-14743-8". Click here for further information.

Table of Contents General Processing Steps Data Preprocessing Transformation of the Data Space
Index
See also: chemical example 

Transformation of the Data Space

If modeling techniques are applied to high-dimensional multivariate problems, most methods fail to deliver a fair model because of the complexity of the data space. Although there is some relationship between the data, it cannot be modeled because the relationship is hidden by too many variables (or, stated from another point of view, the relationship is distributed over too large a number of variables). In this case some special pre-processing of the data may enhance the results considerably. The pre-processing should be applied with the knowledge about the data in mind. Generally speaking, data pre-processing is a means of introducing specific knowledge about the data. In mathematical terms, the pre-processing should transform the data space in a way that (1) less variables are needed for the model, and (2) the relationship between the descriptor variables and the target variable becomes simpler.

An extreme but comprehensible example will demonstrate the idea behind transformation of data space. Suppose you have two classes of objects which are described by three parameters x1, x2 and x3. Class 1 forms a cluster having a shape similar to an ellipsoid. The objects of class 2 are all located outside of the ellipsoid.

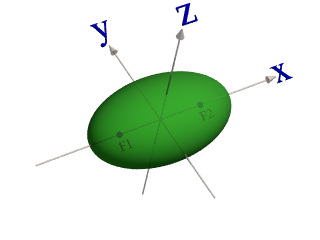
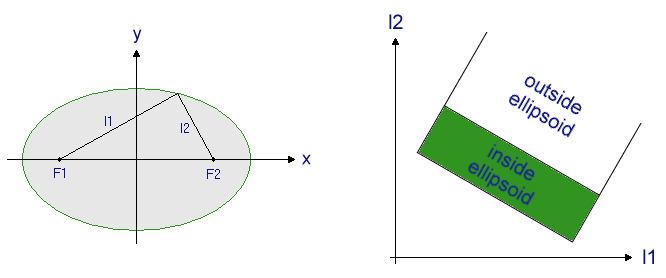
This is a simple example of a classification problem which can only be solved using non-linear methods. It cannot be solved using linear methods such as multiple linear regression. Now, transform the data space (x1, x2, x3) to another space which is defined by two new descriptors l1 and l2. The new descriptors specify the distance of the objects to the foci of the ellipsoid F1 and F2, respectively. Plotting class 1 in the space (l1-l2) transforms the elliptical cluster of class 1 to a rectangular region with a single (!) linear separating surface.

This simple example clearly shows that the transformation of the data space can ease a given problem considerably. In fact, by knowing that cluster 1 forms an ellipsoid, and introducing some knowledge on analytical geometry, we transformed the data space in such a way that (1) the number of necessary variables is decreased and (2)  the non-linear classification task becomes a linear problem (which is easy to solve using well established methods).
 
 
 

Last Update: 2006-Jän-18