 You are working with the text-only light edition of "H.Lohninger: Teach/Me Data Analysis, Springer-Verlag, Berlin-New York-Tokyo, 1999. ISBN 3-540-14743-8". Click here for further information.
You are working with the text-only light edition of "H.Lohninger: Teach/Me Data Analysis, Springer-Verlag, Berlin-New York-Tokyo, 1999. ISBN 3-540-14743-8". Click here for further information.
 You are working with the text-only light edition of "H.Lohninger: Teach/Me Data Analysis, Springer-Verlag, Berlin-New York-Tokyo, 1999. ISBN 3-540-14743-8". Click here for further information. You are working with the text-only light edition of "H.Lohninger: Teach/Me Data Analysis, Springer-Verlag, Berlin-New York-Tokyo, 1999. ISBN 3-540-14743-8". Click here for further information.
|
Table of Contents  Math Background Math Background  Introduction to Probability Introduction to Probability  Additivity rule and mutually exclusive events Additivity rule and mutually exclusive events |
|
| See also: Summation of Probabilities |   |
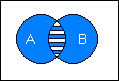
The most simple method to determine the probability of a union of events is to count the sample points of the compound set (provided that the individual probabilities are equal). Sample points which belong to both sets of the compound event are counted only once. If we naively tried to calculate the probability of the union by simply adding the probabilities of the original sets A and B, we would find that the sum of the probabilities of the sets A and B is greater than the probability of the union of A and B. The difference is given by the probability of the intersection of A and B.
From these considerations the probability of the union of two events can be calculated as follows:
P(A) + P (B) = P(A » B) + P(A « B),
so the probability of the union of two events A and B is given by:
We toss a die and define the event A as the set of even numbers, and the event B as the set of numbers less than 3. The probabilities of A, B and the intersection of A and B are: 1/2, 1/3, and 1/6, respectively. The probability of the union of A and B is then P(A » B) = 1/2 + 1/3 - 1/6 = 2/3.
Events A and B are mutually exclusive events, if A « B contains no sample points, i.e. A and B have no sample points in common. In that case, the probability of the union of mutually exclusive events is just the sum of their probabilities.
P(A « B) = P(A) + P(B)
Two coins are tossed and we want to know the probability of getting at least one head. We can represent the event A (at least one head) as the union of the set B (exactly one head) and set C (exactly two heads). Since the events B and C are mutually exclusive, we can just add their probabilities to get the probability of event A:
P(A) = P(B » C) = P(B) + P(C)
P(A) = 1/2 + 1/4 = 3/4
Last Update: 2006-Jšn-18