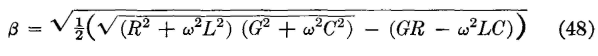Propagation Constant

It is evident that equation 36 contains both real and imaginary terms. Thus, y must also contain real and imaginary components, and therefore it can be written that

If equation 37 is squared,

and

If the real terms and the imaginary terms are equated separately, then

and

When equation 41 is solved for a, it becomes

and, when it is substituted in equation 40, this equation equals

or

and

From this equation β can be found and becomes

Similarly,

The values of X and B can be replaced with the fundamental line constants, and these two equations then become

and

The values of β and α are in units corresponding to the units of the fundamental constants. If R, L, G, and C are expressed per loop mile, then β is the phase constant (formerly called wavelength constant) per loop mile, and α is the attenuation constant per loop mile.

The propagation constant per unit length of a uniform line is¹ the "natural logarithm of the ratio of the current at a point of the line to the current at a second point, at unit distance from the first point along the line in the direction of transmission, when the line is infinite in length, or is terminated in its characteristic impedance." The attenuation constant is¹ "the real part of the propagation constant," and the phase constant is "the imaginary part of the propagation constant."