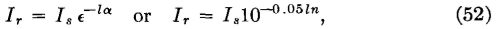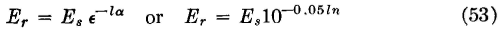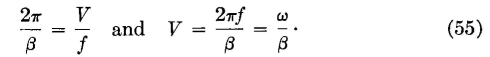The Significance of Z0, a, and ß

As this input current progresses down the line, some of the current is lost at the shunt conductance dG and shunt capacitance dC of Fig. 3. The rate at which the current is weakened, or attenuated, as it progresses down the line is determined by the attenuation constant; that is, by the real part of the propagation constant. Hence, from equations 34 and 37,

where l is the line length, a is in nepers found by equations 37 or 49, and n is in decibels (page 86). Because the current is attenuated the accompanying magnetic field component of the electromagnetic wave also is attenuated.

As the current flows toward the distant end, voltage drops occur along the line wires because of the series resistance dR and the series inductance dL of Fig. 3. The rate at which the voltage is attenuated is determined by the attenuation constant a, and from equations 33 and 37,

where l, α, and n are as explained for equation 52. Because the voltage is attenuated, the accompanying electric field component of the electromagnetic signal wave also is attenuated.

Assume that an alternating signal voltage has just been impressed at the sending end of a line; for instance, at the left of Fig. 3. Before a voltage can exist at the end of a line section, the distributed capacitance of the section must be charged; this requires time, because the charging-current flow is limited by the series resistance and the inductance. As the voltage builds up across one section, the distributed capacitance of the next section starts to charge, and in this way the wave is propagated along the line. Time is, therefore, required for an electromagnetic wave to flow along a line. Thus the instantaneous magnitudes of the currents will not be the same at the various points along a line. The current may be maximum at one point, and zero at another point at the same instant. There is a time phase angle between current at one point and current at another point along the line. Likewise, there will be a time phase angle between the voltage at one point, and the voltage at another point along the line. These phase angles between current at one point and current at another point, or between voltage at one point and voltage at another point, are determined by the phase constant β.

The value of ft (in radians) can be found by equations 37 or 48. The value of radians (when multiplied by 57.3°) determines the difference in phase in degrees. Corresponding points of the electromagnetic wave are 360° apart, and, as Fig. 4 indicates, 360° is one wavelength. Since β is the phase shift per unit length of line, the length of line required to shift the wave 360° or the length of one wavelength is

It is known, however, that λ = V/f, where V is the wave velocity at the frequency /. Thus,