Resonant Transmission Lines

Author: J.B. Hoag

Non-resonant lines are either so very long that the energy has all been lost along the line before reaching the end, or they are terminated by an impedance equal to that of the line so that the energy is all absorbed in the load at the output end and none is reflected. If, however, these conditions are not fulfilled, the waves will be reflected, at least in part, from the output end and travel back toward the generator. If the impedance of the generator is the same as that of the line, the energy will be absorbed at this point. But, if neither input nor output ends are matched to the line, the waves travel back and forth repeatedly to set up a complicated system of waves. This is analogous to moving a piston inside an organ pipe or fog horn. If the length of the line, the pipe, or the horn, is adjusted correctly so that a wave from the source starts out just when the returning wave has reached it and is ready to travel down the system again, the two waves will add to each other, crest for crest, trough for trough. This reinforcement or resonance builds up a much greater final amplitude than that of one wave alone. Under these conditions, the line is said to be resonant to the generator and the waves along it are called standing-waves. In this way the sounding board of a piano reinforces the weak sound waves of the vibrating strings to make them easily heard throughout the room.

When exact resonance has been produced along a line, it will be found that the current at certain points is zero, and remains at zero at all times. These are called current nodes. At other points, one-quarter of a wave-length (λ', not λ) away (halfway between the nodes), the current will be a maximum. These are called current loops or anti-nodes. The voltage across the line also varies from zero to a maximum and back again as one progresses down the line. The voltage loops occur at the same points as the current nodes, and the voltage nodes are at the same place as the current loops.

When exact resonance has not been established, and it never is in practice, the value of the current (or voltage) at a node is not exactly equal to zero. The standing-wave ratio is the ratio of the current (or voltage) at a loop to the value at a node. It is determined by the terminal and by the characteristic impedances. It is equal to the characteristic impedance of the line divided by the terminating impedance or resistance, or the inverse, according to which gives a number greater than 1. A 500-ohm line terminated in a resistance of 50 ohms, or a 50-ohm line terminated in a 500-ohm resistance, both have a standing-wave ratio of 10. If the terminal impedance matches the characteristic line impedance, the standing-wave ratio is unity, all energy passing down the wire is absorbed at the terminus, and there is no reflection at this point. A line in which the standing-wave ratio is about equal to 1 is said to be non-resonant. If this ratio is fairly large, the line is said to be resonant. The losses of an air-insulated parallel-wire transmission line increase slowly from 0.14 db. per wave-length as the standing-wave ratio increases from 1 to about 15, after which they increase rapidly.

Fig. 35 G. Lecher wires are used to measure wave-length (λ')

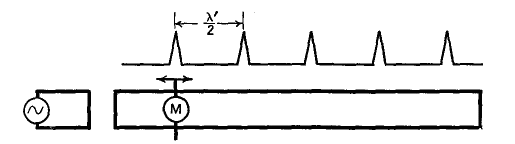
A transmission line may be used to measure the length of the waves. In Fig. 35 G, an r.f. meter M, or a glow-lamp, is shorted across the line and moved along until a maximum reading or glow is observed. The location of this point can be made quite accurately because the peaks are very sharp. M is then moved along the line to a second peak. The distance between the two positions is equal to one-half wave-length. Lines so used are sometimes referred to as Lecher wires.