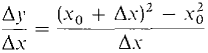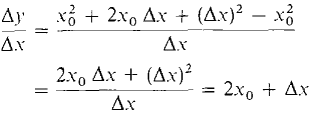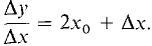Average Slope

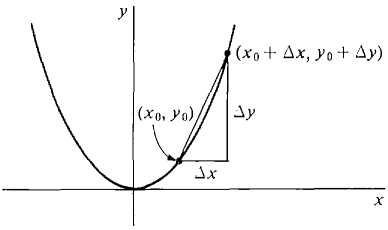
If (x₀, y₀) and (x₀ + Δx, y₀ + Δy) are two points on the curve, then the "average slope" of the curve between these two points is defined as the ratio of the change in y to the change in x,

This is exactly the same as the slope of the straight line through the points (x₀, y₀) and (x₀ + Δx, y₀ + Δy), as shown in Figure 1.4.1.

Let us compute the average slope. The two points (x₀, y₀) and (x₀ + Δx, y₀ + Δy) are on the curve, so

y₀ = x₀²

y₀ + Δy = (x₀ + Δx)².

Subtracting,

Δy = (x₀ + Δx)² - x₀².

Dividing by Δx,

This can be simplified,

Thus the average slope is

Notice that this computation can only be carried out when Δx ≠ 0, because at Δx = 0 the quotient Δy/Δx is undefined.