Actual Slope

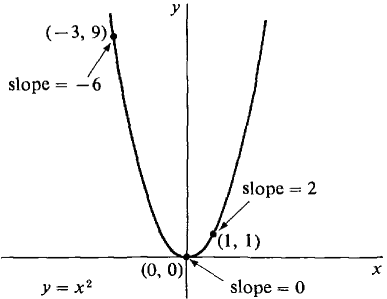
Reasoning in a nonrigorous way, the actual slope of the curve at the point (x₀, y₀) can be found thus. Let Δx be very small (but not zero). Then the point (x₀ + Δx, y₀ + Δy) is close to (x₀, y₀), so the average slope between these two points is close to the slope of the curve at (x₀, y₀);

[slope at (x₀, y₀)] is close to 2x₀ + Δx.

We neglect the term Δx because it is very small, and we are left with

[slope at (x₀, y₀)] = 2x₀.

For example, at the point (0, 0) the slope is zero, at the point (1, 1) the slope is 2, and at the point ( -3, 9) the slope is -6. (See Figure 1.4.2.)