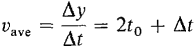Average Velocity

The whole process can also be visualized in another way. Let t represent time, and suppose a particle is moving along the y-axis according to the equation y = t². That is, at each time t the particle is at the point t² on the y-axis. We then ask: what is meant by the velocity of the particle at time t₀? Again we have the difficulty that the velocity is different at different times, and the calculus is needed to answer the question in a satisfactory way. Let us consider what happens to the particle between a time t₀ and a later time t₀ + Δt. The time elapsed is Δt, and the distance moved is Δy = 2t₀ Δt + (Δt)². If the velocity were constant during the entire interval of time, then it would just be the ratio Δy/Δt. However, the velocity is changing during the time interval. We shall call the ratio Δy/Δt of the distance moved to the time elapsed the "average velocity" for the interval;

The average velocity is not the same as the velocity at time t₀ which we are after. As a matter of fact, for t₀ > 0, the particle is speeding up; the velocity at time t₀ will be somewhat less than the average velocity for the interval of time between t₀ and t₀ + Δt, and the velocity at time t₀ + Δt will be somewhat greater than the average.

But for a very small increment of time Δt, the velocity will change very little, and the average velocity Δy/Δt will be close to the velocity at time t₀. To get the velocity v₀ at time t₀, we neglect the small term Δt in the formula

v_ave = 2t₀ + Δt,

and we are left with the value

v₀ = 2t₀.

When we plot y against t, the velocity is the same as the slope of the curve y = t², and the average velocity is the same as the average slope.