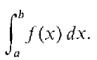Regions under a Curve

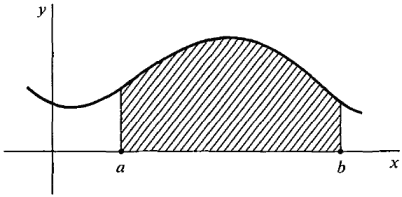
We shall begin our study of the integral calculus in the same way in which we began with the differential calculus-by asking a question about curves in the plane.

Suppose f is a real function continuous on an interval I and consider the curve y = f(x). Let a < b where a, b are two points in I, and let the curve be above the x-axis for x between a and b; that is, f(x) ≥ 0. We then ask: What is meant by the area of the region bounded by the curve y = f(x), the x-axis, and the lines x = a and x = b? That is, what is meant by the area of the shaded region in Figure 4.1.1? We call this region the region under the curve y = f(x) between a and b.

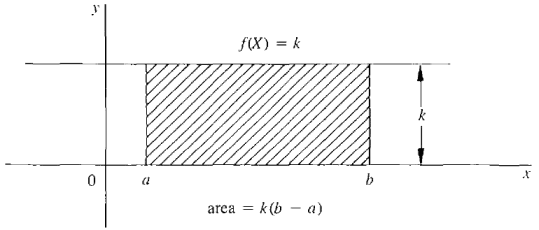
Figure 4.1.1 The Region under a Curve

The simplest possible case is where f is a constant function; that is, the curve is a horizontal line f(x) = k, where k is a constant and k ≥ 0, shown in Figure 4.1.2. In this case the region under the curve is just a rectangle with height k and width b - a, so the area is defined as

Area = k · (b - a).

The areas of certain other simple regions, such as triangles, trapezoids, and semicircles, are given by formulas from plane geometry.

Figure 4.1.2

The area under any continuous curve y = f (x) will be given by the definite integral, which is written