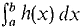Infinite Sum Theorem - Definition

In Chapter 4 we obtained the formula

for the area of the region bounded by the x-axis, the curve y = f(x), and the lines x = a and x = b.

In this chapter we shall obtain integral formulas for several other quantities arising in geometry and physics, such as volumes, curve lengths, and work. We begin with the Infinite Sum Theorem, which will be useful in justifying these formulas. It tells when a given function B(a, b) is equal to the definite integral

Any two infinitesimals are infinitely close to each other. The following definition helps us to keep track of how close to each other they are.

In Figure 6.1.1, an infinitesimal microscope within an infinitesimal microscope is used to show ε as δ (compared to Δx).

Figure 6.1.1: ε ≈ δ (compared to Δx)