| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Integral Integral  The Definite Integral The Definite Integral  Riemann Sum Riemann Sum |
||||||||






|
||||||||
Riemann Sum
Before plunging into the detailed definition of the integral, we outline the main ideas. First, the region under the curve is divided into infinitely many vertical strips of infinitesimal width dx. Next, each vertical strip is replaced by a vertical rectangle of height f(x), base dx, and area f(x) dx. The next step is to form the sum of the areas of all these rectangles, called the infinite Riemann sum (look ahead to Figures 4.1.3 and 4.1.11). Finally, the integral
The infinite Riemann sum, being a sum of rectangles, has an infinitesimal error. This error is removed by taking the standard part to form the integral. It is often difficult to compute an infinite Riemann sum, since it is a sum of infinitely many infinitesimal rectangles. We shall first study finite Riemann sums, which can easily be computed on a hand calculator. Suppose we slice the region under the curve between a and b into thin vertical strips of equal width. If there are n slices, each slice will have width ∆x = (b - a)/n. The interval [a, b] will be partitioned into n subintervals
where
The points x0, x1,..., xn are called partition points. On each subinterval [xk-1, xk], we form the rectangle of height f(xk-1). The kth rectangle will have area
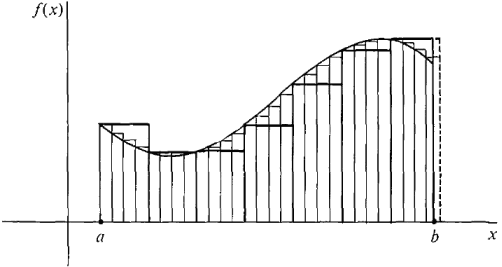
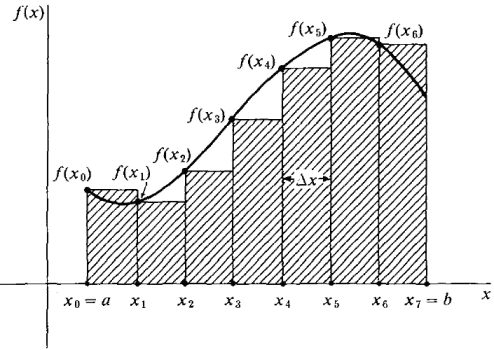
From Figure 4.1.3, we can see that the sum of the areas of all these rectangles will be fairly close to the area under the curve. This sum is called a Riemann sum and is equal to
It is the area of the shaded region in the picture. A convenient way of writing Riemann sums is the "Σ-notation" (Σ is the capital Greek letter sigma),
Figure 4.1.3 The Riemann Sum The a and b indicate that the first subinterval begins at a and the last subinterval ends at b. We can carry out the same process even when the subinterval length Δx does not divide evenly into the interval length b-a. But then, as Figure 4.1.4 shows, there will be a remainder left over at the end of the interval [a, b], and the Riemann sum will have an extra rectangle whose width is this remainder. We let n be the largest integer such that a + n Δx ≤ b, and we consider the subintervals [x0, x1],..., [xn-1, xn], [xn, b], where the partition points are x0 = a, x1 = a + Δx, x2 = a + 2 Δx,..., xn = a + n Δx, b.
Figure 4.1.4 xn will be less than or equal to b but xn + ∆x will be greater than b. Then we define the Riemann sum to be the sum
Thus given the function f, the interval [a, b], and the real number ∆x > 0, we have defined the Riemann sum DEFINITIONLet a < b and let ∆x be a positive real number. Then the Riemann sum
where n is the largest integer such that a + n ∆x ≤ b, and x0 = a, x1 = a + ∆x, ..., xn = a + n ∆x, b are the partition points. If xn = b, the last term f(xn)(b - xn) is zero. The Riemann sum
The symbol x which appears in the expression is called a dummy variable (or bound variable), because the value of From Figure 4.1.5 it is plausible that by making ∆x smaller we can get the Riemann sum as close to the area as we wish.
Figure 4.1.5
|
||||||||
Home  Integral Integral  The Definite Integral The Definite Integral  Riemann Sum Riemann Sum |
||||||||
Last Update: 2010-11-26


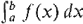 is defined as the standard part of the infinite Riemann sum.
is defined as the standard part of the infinite Riemann sum.
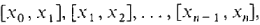
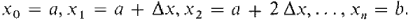
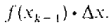
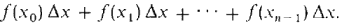
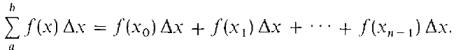

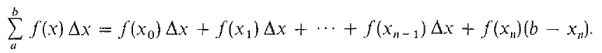
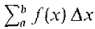 . We repeat the definition more concisely.
. We repeat the definition more concisely. is defined as the sum
is defined as the sum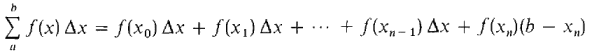
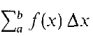 is a real function of three variables a, b, and Δx,
is a real function of three variables a, b, and Δx,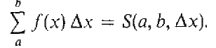
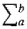 f (x) Δx does not depend on x. The dummy variable allows us to use more compact notation, writing f(x)∆x just once instead of writing f(x0)∆x, f(x1) ∆x, f(x2) ∆x, and so on.
f (x) Δx does not depend on x. The dummy variable allows us to use more compact notation, writing f(x)∆x just once instead of writing f(x0)∆x, f(x1) ∆x, f(x2) ∆x, and so on.