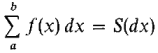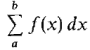Infinite Riemann sum

Our next step is to take Δx to be infinitely small and have an infinite Riemann sum. How can we do this? We observe that if the real numbers a and b are held fixed, then the Riemann sum

is a real function of the single variable Δx. (The symbol x which appears in the expression is a dummy variable, and the value of

depends only on Δx and not on x.) Furthermore, the term

is defined for all real Δx > 0. Therefore by the Transfer Principle,

is defined for all hyperreal dx > 0. When dx > 0 is infinitesimal, there are infinitely many subintervals of length dx, and we call

an infinite Riemann sum (Figure 4.1.11).

Figure4.1.11 Infinite Riemann Sum

We may think intuitively of the Riemann sum

as the infinite sum

f(x₀) dx + f (x₁) dx + ... + f(x_H-1) dx + f(x_H)(b - x_H)

where H is the greatest hyperinteger such that a + H dx ≤ b. (Hyperintegers are discussed in Section 3.8.) H is positive infinite, and there are H + 2 partition points x₀, x₁, ... , x_H, b. A typical term in this sum is the infinitely small quantity f(x_K)dx where K is a hyperinteger, 0 ≤ K < H, and x_K = a + K dx.

The infinite Riemann sum is a hyperreal number. We would next like to take the standard part of it. But first we must show that it is a finite hyperreal number and thus has a standard part.