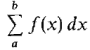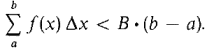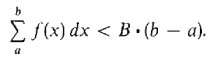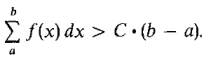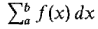| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |
|
Home  Integral The Definite Integral Theorem: Infinite Riemann Sum |
|
 Search the VIAS Library | Index
|
  |
Theorem: Infinite Riemann Sum
THEOREM 1
Let f be a continuous function on an interval I, let a < b be two points in I, and let dx be a positive infinitesimal. Then the infinite Riemann sum
is a finite hyperreal number. PROOF Let B be a real number greater than the maximum value of f on [a,b].
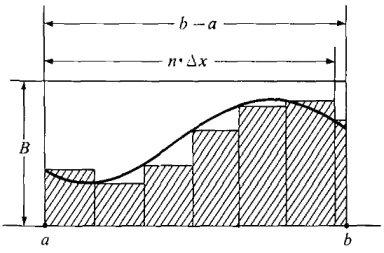
Figure 4.1.12 Consider first a real number Δx > 0. We can see from Figure 4.1.12 that the finite Riemann sum is less than the rectangular area B · (b - a);
Therefore by the Transfer Principle,
In a similar way we let C be less than the minimum of f on [a, b] and show that
Thus the Riemann sum
|
|
| Home Integral The Definite Integral Theorem: Infinite Riemann Sum |
|
Last Update: 2010-11-26