| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Applications of the Integral Applications of the Integral  Area of a Surface of Revolution Area of a Surface of Revolution  Parametic Equations Parametic Equations |
|||||






|
|||||
Parametic Equations
When a curve is given by parametric equations we get a formula for surface area of revolution analogous to the formula for lengths of parametric curves in Section 6.3. Let x = f(t), y = g(t), a ≤ t ≤ h be a parametric curve in the first quadrant such that the derivatives are continuous and the curve does not retrace its path (Figure 6.4.10).
Figure 6.4.10 AREA OF SURFACE OF REVOLUTION
To justify this new formula we observe that an infinitesimal piece of the surface is almost a cone frustum of radii x, x + Δx and slant height Δs. Thus compared to Δt,
The Infinite Sum Theorem gives the desired formula for area. This new formula reduces to our first formula when the curve has the simple form y = f(x). If y = f(x), a ≤ x ≤ b, take x = t and get
Similarly, if x = g(y), a ≤ y ≤ b, we take y = t and get the formula
|
|||||
Home  Applications of the Integral Applications of the Integral  Area of a Surface of Revolution Area of a Surface of Revolution  Parametic Equations Parametic Equations |
|||||
Last Update: 2010-11-25


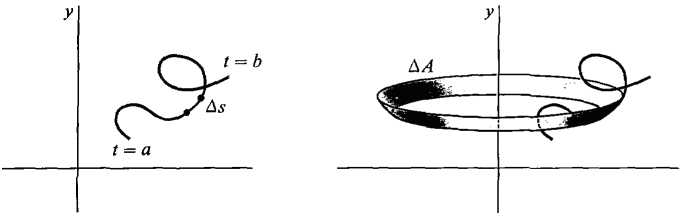
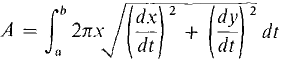 (rotating about y-axis).
(rotating about y-axis).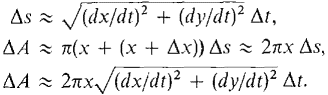
 (about y-axis).
(about y-axis).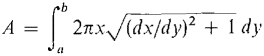 (about y-axis).
(about y-axis).