Area of Surface of Revolution

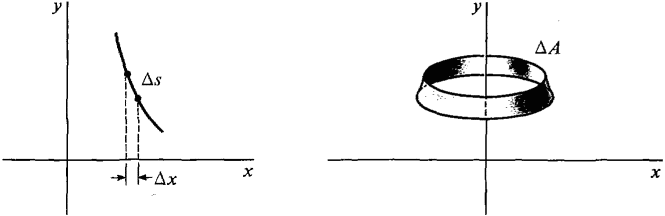
A surface of revolution can be sliced into frustums in the same way that a solid of revolution can be sliced into discs or cylindrical shells. Consider a smooth curve segment

v = f(x), a ≤ x ≤ b

in the first quadrant. When this curve segment is rotated about the y-axis it forms a surface of revolution (Figure 6.4.5).

Figure 6.4.5

Here is the formula for the area.

AREA OF SURFACE OF REVOLUTION

(rotating about y-axis).

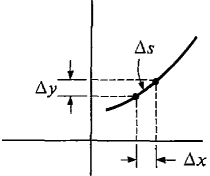
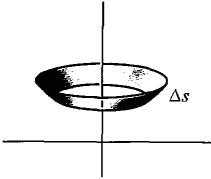
To justify this formula we begin by dividing the interval [a, b] into infinitesimal subintervals of length Δx. This divides the curve into pieces of infinitesimal length Δs. When a piece Δs of the curve is rotated about the x-axis it sweeps out a piece of the surface, ΔA (Figure 6.4.6). Since Δs is almost a line segment, ΔA is almost a cone frustum of slant height Δs, and bases of radius x and x + Δx. Thus compared to Δx,

Then by the Infinite Sum Theorem,

Figure 6.4.6

Example 1: Line Segment

Example 2: Curve

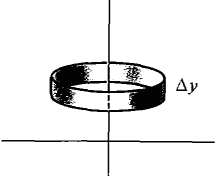
In finding a formula for surface area, why did we divide the surface into frustums of cones instead of into cylinders (as we did for volumes)? The reason is that to use the Infinite Sum Theorem we need something which is infinitely close to a small piece ΔA of area compared to Δx. The small frustum has area

(2x + Δx)n Δs

which is infinitely close to ΔA compared to Δx because it almost has the same shape as ΔA (Figure 6.4.9). The small cylinder has area 2xπ Δy. While this area is infinitesimal, it is not infinitely close to ΔA compared to Δx, because on dividing by Δx we get

Figure 6.4.9(a): frustum

Figure 6.4.9: cylinder

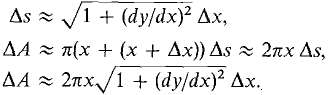
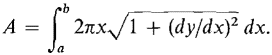
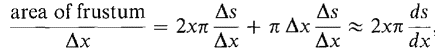
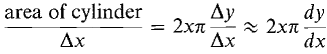
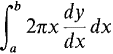Approximating the surface by small cylinders would give us the different and incorrect value for the surface area.