| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Applications of the Integral Applications of the Integral  Improper Integrals Improper Integrals  Half Opened Intervals Half Opened Intervals |
|||||||






|
|||||||
Half Opened Intervals
Improper integrals are defined as follows. DEFINITION Suppose f is continuous on the half-open interval (a, b]. The improper integral of f from a to b is defined by the limit
If the limit exists the improper integral is said to converge. Otherwise the improper integral is said to diverge. The improper integral can also be described in terms of definite integrals with hyperreal endpoints. We first recall that the definite integral
is a real function of two variables u and v. If u and v vary over the hyperreal numbers instead of the real numbers, the definite integral
Here is the description of the improper integral using definite integrals with hyperreal endpoints. Let f be continuous on (a, b]. (1) (2)
Notice that we use the same symbol for both the definite and the improper integral. The theorem below justifies this practice.
|
|||||||
Home  Applications of the Integral Applications of the Integral  Improper Integrals Improper Integrals  Half Opened Intervals Half Opened Intervals |
|||||||
Last Update: 2006-11-05


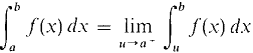
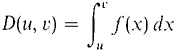
 f(x) dx stands for the natural extension of D evaluated at (u, v),
f(x) dx stands for the natural extension of D evaluated at (u, v),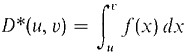
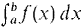 = S if and only if
= S if and only if 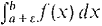 ≈ S for all positive infinitesimal ε.
≈ S for all positive infinitesimal ε. = ∞ (or -∞) if and only if
= ∞ (or -∞) if and only if 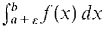 is positive infinite (or negative infinite) for all positive infinitesimal s.
is positive infinite (or negative infinite) for all positive infinitesimal s.