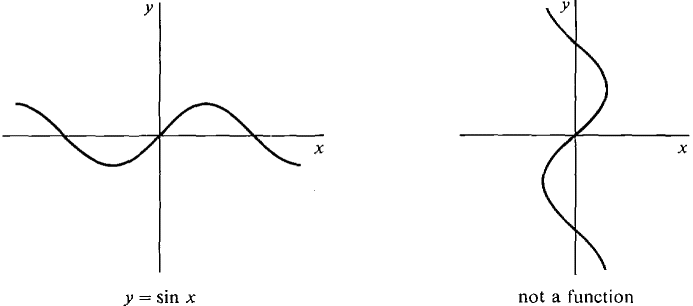| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |
|
Home  Trigonometric Functions Inverse Trigonometric Functions Theorem 1: Inverse Function |
|
 Search the VIAS Library | Index
|
  |
Theorem 1: Inverse Function
THEOREM 1 f has an inverse function if and only if f is one-to-one. PROOF The following statements are equivalent. (1) f is a one-to-one function. (2) For every y, either there is exactly one x with f(x) = y or there is no x with f(x) = y. (3) The equation y = f(x) determines x as a function of y. (4) f has an inverse function. COROLLARY Every function which is increasing on its domain I has an inverse function. So does every function decreasing on its domain I. PROOF Let f be increasing on I. For any two points x1 ≠ x2 in I, the value of f at the smaller of x1, x2 is less than the value of f at the greater, so f(x1) ≠ f(x2). For example, the function y = x2 is not one-to-one because (-1)2 = 12, whence it has no inverse function. The function y = x2, x ≥ 0, is increasing on its domain [0, ∞) and thus has an inverse. Now let us examine the trigonometric functions. The function y = sin x is not one-to-one. For example, sin 0 = 0, sin π = 0, sin 2π = 0, etc. We can see in Figure 7.3.3 that the inverse relation of y = sin x is not a function.
Figure 7.3.3 However, the function y = sin x is increasing on the interval [ - π/2, π/2], because its derivative cos x is ≥ 0. So the sine function restricted to the interval [-π/2, π/2], y = sin x, - π/2 ≤ x ≤ π/2, has an inverse function shown in Figure 7.3.4. This inverse is called the arcsine function. It is written x = arcsin y. Verbally, arcsin y is the angle x between - π/2 and π/2 whose sine is y.
Figure 7.3.4
|
|
| Home Trigonometric Functions Inverse Trigonometric Functions Theorem 1: Inverse Function |
|
Last Update: 2006-11-05