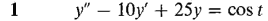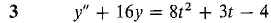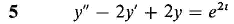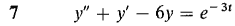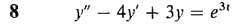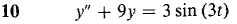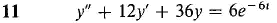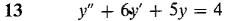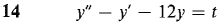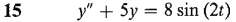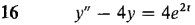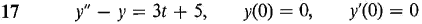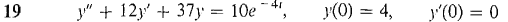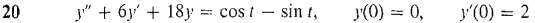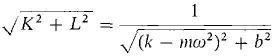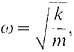Problems (Particular and General Solution of Differential Equations)

In Problems 1-12, find a particular solution of the given differential equation.

In Problems 13-16, find the general solution of the given differential equation.

In Problems 17-20, find the particular solution of the initial value problem.

21            A mass-spring system mx" + bx' + kx = 689 cos (2f) has an external force of 689 cos (2t) dynes, spring constant k = 29, damping constant b =4, and mass m = 1 gm. Find the general solution for the motion of the spring and the steady state part of the solution.

22            A mass-spring system mx" + bx' + kx = 2 sin t has an external force of 2 sin t dynes, spring constant k = 24, damping constant b = 12, and mass m = 3gm. Find the general solution for the motion of the spring and the steady state part of the solution.

23            In the mass-spring system

(5)                                        my" + by' + ky = cos (ωt),

where m, b, and k are positive, show that the steady state part of the solution has amplitude

24            In Problem 23, show that the frequency ω in the forcing term for which the steady state has the largest amplitude is

and the largest amplitude is 1/b. This frequency ω is called the resonant frequency.

25            Using Problem 24, find the resonant frequency for the mass-spring system

y" + 6y' + 25y = cos (ωt).