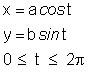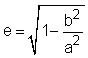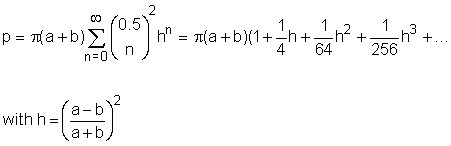Ellipse

The Compendium Geometry is an eBook providing facts, formulas and explanations about geometry.

Home Analytic Geometry Circle and Ellipse Ellipse
See also: Properties of a Right Triangle
Search the VIAS Library \| Index
Ellipse An ellipse is the curve which develops when drawing all points in a plane whose distances l_a and l_b from the focal points F₀ and F₁ sum up to the constant 2a: l_a + l_b = 2a The line segment 2a is called the major axis of the ellipse, the segment 2b is called the minor axis. The line passing through the foci F₀ and F₁ is called the major axis, the line perpendicular to it and passing through the center C of the ellipse is called the minor axis. The length of the major axis is 2a, the length of the minor axis is 2b. If the two foci coincide, then the ellipse is a circle. Most properties of ellipses also apply to circles as a special case. In Cartesian coordinates, if the center C of the ellipse is given by [c_x, c_y], the ellipse can be defined as An ellipse may also be described by the following parametric equations: The shape of an ellipse can be expressed by the eccentricity e of the ellipse, which is defined by The eccentricity is a positive number between 0 and 1. For e=0 the ellipse becomes a circle, for e=1 the ellipse degenerates to a line along the major axis. The distance between the foci is 2ae. In order to calculate the perimeter of an ellipse one has to calculate the elliptic integral of the second kind. This integral can be calculated by the following series expansion: A good approximation of the perimeter for small h values is given by The area A of an ellipse is given by A = abπ.
Home Analytic Geometry Circle and Ellipse Ellipse

Last Update: 2010-12-06