| The Compendium Geometry is an eBook providing facts, formulas and explanations about geometry. |

|

Home  Analytic Geometry Analytic Geometry  Triangle Triangle  Properties of a Right Triangle Properties of a Right Triangle |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
| See also: Triangle - General Definitions, Properties of Arbitrary Triangles, Altitudes of a Triangle, Isosceles Triangle, Pythagorean Theorem, Thales' Theorem, Incircle and Angle Bisectors of a Triangle, Median and Centroid of a Triangle, Ellipse | |||||||||||||||||||||||||||||||||||||||||||||||||||||






|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
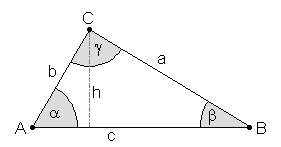
Properties of a Right TriangleA right triangle has one angle (the angle γ at the point C by convention) of 90 degrees (π/2). The longest side, which is opposite to the angle γ is called hypothenuse (the word derives from the Greek hypo - "under" - and teinein - "to stretch"). The legs of a right triangle (i.e. the sides adjacent to the right angle) are also known as catheti (singular: cathetus). In German, the two legs are denoted using different terms: Ankathete (adjacent cathetus) and Gegenkathete (opposite cathetus) denote the legs adjacent to and opposite the (non-right) angle in question, respectively.
sin = opposite / hypothenuse
Further the altitude of the triangle h is given by h = ab/c, the radius of the incircle is defined byri = (a + b - c)/2, the radius of the circumcircle is given byrcc = c/2, and the center of gravity is at one third of the height h.If two parameters of a right triangle are known, all other parameters can be calculated. The following table contains the most important parameters (three sides a, b, c, two angles α and β and the area).
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
Home  Analytic Geometry Analytic Geometry  Triangle Triangle  Properties of a Right Triangle Properties of a Right Triangle |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
Last Update: 2011-01-11


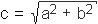
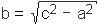
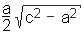

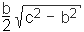
 cot(α)
cot(α)