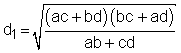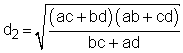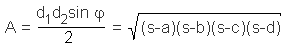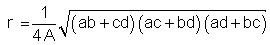The Compendium Geometry is an eBook providing facts, formulas and explanations about geometry.

Home Analytic Geometry Quadrilateral Cyclic Quadrilateral
See also: Quadrilateral - General Definitions, Tangential Quadrilateral 
del.icio.us Reddit Facebook StumbleUpon MySpace Twitter Search the VIAS Library  |  Index

Cyclic Quadrilateral

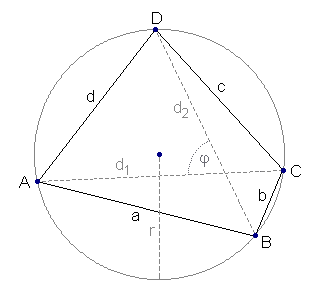A cyclic quadrilateral is a quadrilateral whose vertices lie on a circle. The opposite angles of a cyclic quadrilateral sum to 180 degrees. Please note that the inverse is also true: the vertices of a quadrilateral lie on a circle if the opposite angles sum up to 180°.

A quadrilateral that has both an incircle and a circumcircle is known as a bicentric quadrilateral.

The length of the diagonals is given by:


The product of the two diagonals is equal to the sum of the products of the opposite sides (Ptolemy's theorem):

d1d2 = ac+bd

The area A of the cyclic quadrilateral is defined by

with s equal to the semiperimeter s = (a+b+c+d)/2. Please note that for any quadrilateral of given side lengths, the area of a cyclic quadrilateral is maximal.

The radius r of the circumcircle is given by

Home Analytic Geometry Quadrilateral Cyclic Quadrilateral

Last Update: 2010-12-06